はじめに
中学生のときから不思議だと思っていたことをこの前ふと呟いたところ、どうやらほとんどの方がこの不思議さを理解できないことに気付きました。
よく英語の文法問題で
A: I robbed the bank yesterday.
B: Oh, did ___?
に入る語を答えなさいってあるけど、これが ‘I’ ではなく ‘you’ になるのって、やっぱり不思議なことだよなぁと常々思う。というか自分は中学生のときボーッとしてる ‘I’ って書いちゃったしね。
ところで、うっかり「これが ‘I’ ではなく ‘you’ になる」などと書いていますが、これは誤りです。申し訳ありません。正確には、たとえば
- Oh, did I?
- Oh, did you?
- No, I didn’t.
- Yes, you did.
の全てが A の発言に対する応答として適切なものになります。一般的に 2 と 4 が正解だとされるようですが、1 と 3 も当然可能です。これらを正当化する文脈は割とありふれているのですが、どうやらなかなか思い付きにくいようなので簡単な例を述べてしまいます。
幻聴の症状には、一人称・二人称・三人称のパターンがすべて存在することが一般に知られています。したがって、幻聴と妄想に悩まされている B さんが、本当は B さんの脳内にある A さんからの「私は昨日銀行強盗をしたのだ」という声を聞いて、「なんと、私はそんなことをしてしまったのか?(なんてことだ!)」と呟けば “Oh, did I?” (1) と翻訳されるべきものですし、「いや、私はそんなことをしていない」と反論すれば “No, I didn’t.” (3) と翻訳されるべきものになります。ここで注意すべきは、この不思議さを「人称の不思議さ」ではなく「幻聴の不思議さ」と置き換えてはならないことです。もちろん幻聴は(読んだことはないのですが)ラカンなどによってさまざまな議論が行われてきた不思議な症状ではありますが、神でも悪霊でも、脳への磁気刺激でも催眠でも、そもそも普通の文脈(たとえば頭部の繋がった結合双生児)でも想定することができます。
屁理屈の成立しえない純粋な文法問題を作成するというのは非常に困難であり、若林・根岸 (1993) は次のようにその困難さを見事に物語っています。
それにしても、「語形変化」を問うテストを作るのは難しい。たとえば、The sun (rise) in the east. を与えて rises と解答させようとしても、たとえば rising という答えが出てきたとき、本当にこれを零点にすることができるのであろうか。「東の空に昇りつつある太陽」ということであれば、これで正解であろう。rose でもよい。どこかの架空の国で、ある恒星(sun)がいつもならば北から出てくるのに、今日に限って東から昇った、ということもあり得るのである。rise のままでもよい。「わが恒星よ、東より昇れかし」という意味になり得る。
ですから、作成者側も「試験という形式自体に、ある程度のコンテクストに依存した要素が必然的に内包されてしまうのだ」という一種の諦観を持ちながらも解答がなるべく一意に定まるよう心がける一方で、回答者側もその諦観を持ちつつ「それでも空気を上手に読んで作成者とのコミュニケーションを成立させよう」という気概を持つことが自らの高貴さを示すことになるのでしょう。これは、たとえば「数列 $2,4,6,\dots$ の一般項 $a_n$ $(n\geq1)$ を求めよ」という問題に $a_n=2n$ ではなく
$$a_n=2\cdot\dfrac{(n-2)(n-3)}{(1-2)(1-3)}+4\cdot\dfrac{(n-1)(n-3)}{(2-1)(2-3)}+6\cdot\dfrac{(n-1)(n-2)}{(3-1)(3-2)}$$
と答える(これが $n=1,2,3$ において正しいことは代入してみればそのカラクリが即座に理解できます)のと似たような話でもあります。
クリプキはたし算(plus)ならぬクワス算(quus)を例に「規則のパラドックス」を提示しました*1が、それは素朴な意味では起こり得ないのに対して、それと本質的に同型な、如上の数列の一般項についてのパラドックスは実際によく起こっています。そもそも、数学で「$\dots$」という記号が使われる際にはほとんど必ずこのパラドックスがついて回るので、ロジック(数理論理学や数学基礎論と呼ばれる分野)の方々はここらへんの事情に非常に気を払っているようです。たとえばシグマ記号はよく $\dots$ を用いて定義されますが、正しくは漸化式を用いて帰納的に定義されるべきものです。しかし本稿で論じたいのは「問題」としての性質ではなく「人称」についての不思議さだけなので、さっそく話題を移ることにしましょう。
何が不思議なのか?
この不思議さは、実は永井 (2016) の第12章「時間の矛盾を人称や様相と同型である側面において考察する」の「マクタガートの言い換えを人称に適用する」で完璧に表現されているのです。
私は、いま対面して話している相手から見れば「あなた」であり、またどこかで私のことを話題にしている人から見れば「彼」であるが、それでも現実には「私」である。どんなに他人たちから、それはおまえにとってそうであるにすぎないのだ、と言われようとも、一面ではやはり、この「とって」は断固拒否されねばならないし、現実に拒否されてもいる。なぜなら、これが究極において拒否されていなければ、正当に「私」と発話するたくさんの人間のうちどれが端的に私であるのか、それを識別することができないはずだからである。それはおまえにとってそうであるだけなのだよ、といくら言われても、その「とって」はどこまでも拒否されねばならないし、現実に拒否されているのである。
他面ではもちろん、他人たちの視点を受け入れて、「そうだ、私にとって私であるにすぎない」と認めなければならないし、現実に認めてもいる。なぜなら、これを認めなければ、私にとって対話相手が「あなた」であるのと同様に対話相手にとっては私が「あなた」である、といったようなコミュニケーション成立の根本前提そのものが成り立たなくなってしまうからである。この不可避的な二面性によって、人称(person)にも「矛盾」があることは明らかである。
この矛盾の正体を(詳しい議論やマクタガートの主張については実際に本書を読んでいただきたいのですが)永井は次のように論じます。
それ[私が私でしかありえないことと彼でもあなたでもありうることとの矛盾]を、次の二つの捉え方の矛盾と見ることもできる。
一つの捉え方はこうだ……人物の存在の仕方には彼(彼女)としてとあなたとしての二種類しかなく、私とはその二種類の設定をする任意の主体のことでしかない。だから、私は彼(彼女)を彼(彼女)として、あなたをあなたとして捉えることができるが、彼(彼女)やあなたは私を私として捉えることはできず、彼(彼女)は私を彼(彼女)として捉え、あなたは私をあなたとして捉えるしかない。彼(彼女)にとってもあなたにとっても、「私」といえば自分自身のことでしかない……私は他者から捉えられる場合には彼(彼女)かあなたとなるほかはない。
もう一つの捉え方はこうだ……現実に私と私でない人物が存在する。これは変わることのない現実であるから、彼(彼女)から捉えられようと、あなたから捉えられようと、私は私のままである。彼(彼女)やあなたが私であるというのは現実とは異なる仮想上のことでしかない。
現実に、われわれはこの二つの捉え方の矛盾を生きており、生きていかざるをえない。このことは、世界というものは客観的な一枚の絵に描けるようなのっぺりした(金太郎飴的な)あり方をしていない、ということを示している。人称にかんしても時制にかんしても、この矛盾こそが人生のあらゆる問題の根源である(*)。
*単純な例ではあるが、カントのいわゆる「定言命法」は人称にかんして、前の段落の「一つの捉え方」を取って「もう一つの捉え方」のほうを拒否することを要求するものである……
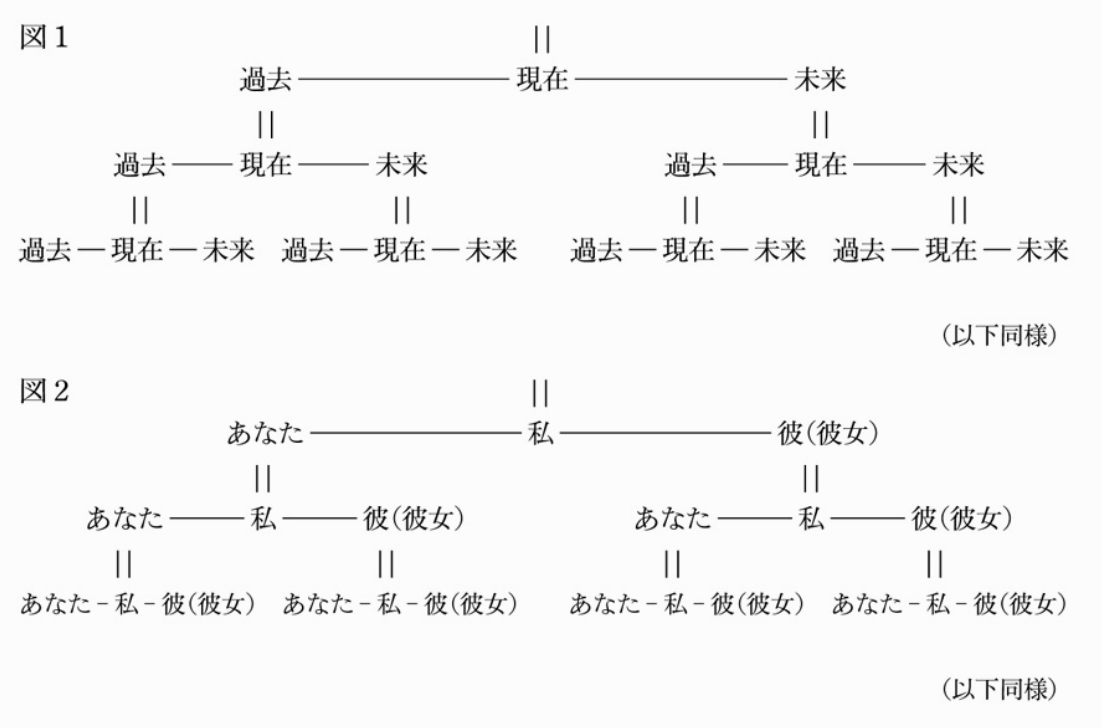
なんとも心温まる話です。問題の原因はまさにここにあると言えるでしょう。そしてこの人称を成立させるロゴスの本質構造こそが累進構造に他なりません。
参考文献
永井均. (2016). 『存在と時間: 哲学探究1』. 文藝春秋.
若林俊輔, 根岸雅史. (1993). 『無責任なテストが「落ちこぼれ」を作る: 正しい問題作成への英語授業学的アプローチ』. 大修館書店.
*1:そういえば、かけ算で規則のパラドックスを作りたいのだったら、たとえば mod 999999999 で行われる「くゎけ算」を考えればいいんでしょうか。