訳者序
本稿は Freudenthal, H; van der Waerden, B. L. (1947). “Over een bewering van Euclides” (“On an assertion of Euclid”), Simon Stevin, 25: 115–121 の日本語訳を 10 年留保によって公開したものである.本文中の訳注は亀甲括弧〔……〕に入れて提示した.訳文の作成にあたっては,恩師の N 先生に丁寧で的確な助言を多くいただいた.
本文
『原論』第13巻では5つの正多面体が扱われており,最後には「いま述べた5つの図形〔正4面体,正6面体,正8面体,正12面体,正20面体〕以外に,等辺等角で互いに等しい図形にかこまれる他の図形はつくられない」という主張で締めくくられている.
ディクステルホイスが指摘しているように(De Elementen van Euclides IIのp. 267の注),この主張を文字通りに解釈すると,すべての頂点において接する面の数が等しいという条件が抜けているので偽となる.たとえば,20面体をいくらでも重ねたり,8面体や4面体をいくつかの面の上に置いたりできる.可能な図形は明らかに無限個存在する.
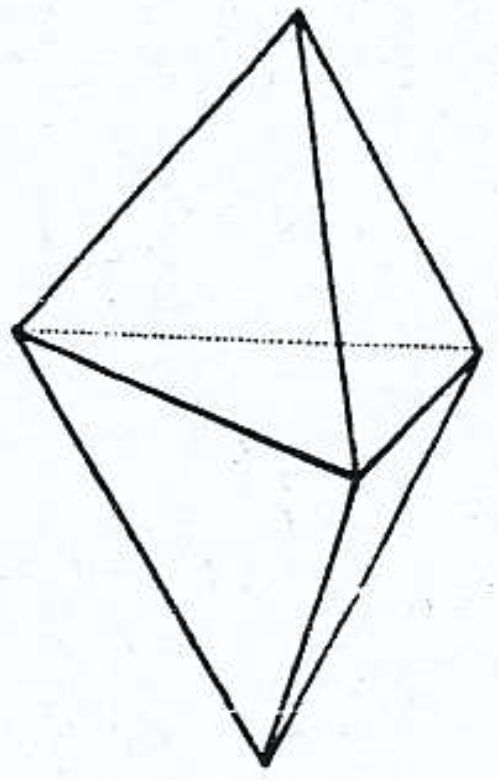
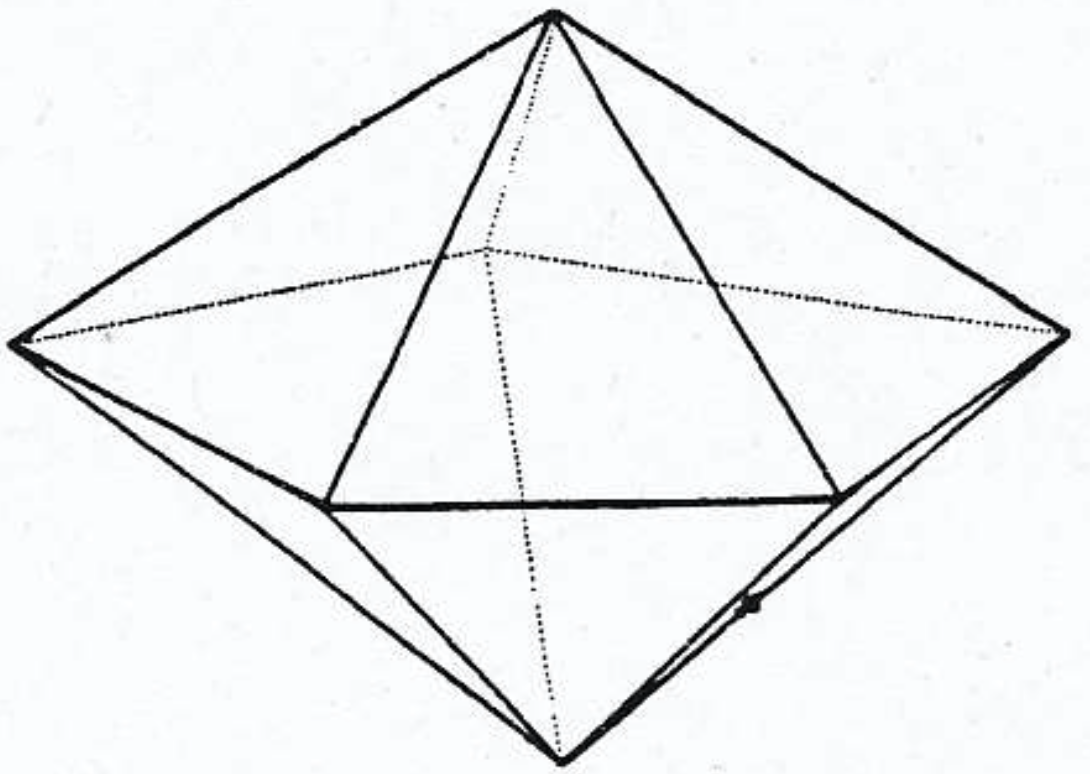
しかし,凸多面体に限定すると,可能な図形は有限個となる.最も簡単な例は2つの「双角錐」*2,つまり6面体と10面体である.これらの立体は,すべての辺が等しい2つの3角錐および5角錐を,それぞれ底面どうしで貼り合わせることで作られる(図1・図2参照).
本論文の目的は,面どうしが合同な正多角形である凸体をすべて決定することである.
面が4角形や5角形であれば,各頂点に面は3つずつ集まるしかないので,立方体と正12面体のみが得られる.そのため,面が3角形であると仮定してよい.
3つや4つ,5つの3角形が集まる頂点を,それぞれ3次の頂点,4次の頂点,5次の頂点と呼ぶ.$a_3$ を3次の頂点の数,$a_4$ を4次の頂点の数,$a_5$ を5次の頂点の数とする.このとき,辺の数は
\begin{equation}
b=\frac{3a_3+4a_4+5a_5}{2}
\end{equation}
であり,面の数は
\begin{equation}
c=\frac{3a_3+4a_4+5a_5}{3}
\end{equation}
である.オイラーの凸体定理により
\begin{equation}
a_3+a_4+a_5-b+c=2
\end{equation}
であるから,
\begin{equation}
\frac{3}{6}a_3+\frac{2}{6}a_4+\frac{1}{6}a_5=2\notag
\end{equation}
すなわち
\begin{equation}
3a_3+2a_4+a_5=12
\end{equation}
となる.この方程式の整数解は有限個である.解 $(4,0,0)$, $(0,6,0)$, $(0,0,12)$ はよく知られた正多面体である.ここでは,まず $a_3>0$ の解を求め,次に $a_3=0$ の解を求める.
$a_3>0$ の場合は調べやすい.すなわち,3次の頂点が存在すれば,その点で交わる3つの3角形によって4面体が定まる.この4面体を切り落とすと,与えられた立体よりも頂点が1つ,面が3つ少ない*3立体が残る.このようにして,4面体が1つだけ残るか $a_3=0$ となるまでこの操作を続けることができる.そのため,与えられた立体は,4面体だけを組み合わせるか,3次の頂点をもたない立体の面に4面体を組み合わせることによって作ることができる.しかし,3つ以上の4面体をつなげると立体は凸でなくなり,〔次の例外を除いて〕4次の頂点や5次の頂点を含む面に4面体をつなげても立体は凸でなくなる.唯一の例外として4面体の付いた8面体があるが,その場合は面どうしが同一平面上に存在するので,頂点に接する面がひし形になってしまう.したがって,ここでの〔正多面体以外で $a_3>0$ となる〕凸体は図1の6面体のみである.
$a_3=0$ では,8面体と20面体*4に加えて,次のような解が得られる.
| 番号 | $a_3$ | $a_4$ | $a_5$ | 面の数 |
|---|---|---|---|---|
| 1) | 0 | 1 | 10 | 18 |
| 2) | 0 | 2 | 8 | 16 |
| 3) | 0 | 3 | 6 | 14 |
| 4) | 0 | 4 | 4 | 12 |
| 5) | 0 | 5 | 2 | 10 |
1)の場合は不可能である.実際,4次の頂点 $A$ から始めて,$A$ の周りに5次の頂点 $B$, $C$, $D$, $E$ を輪状に並べると,図3(中心投影図)が得られる.
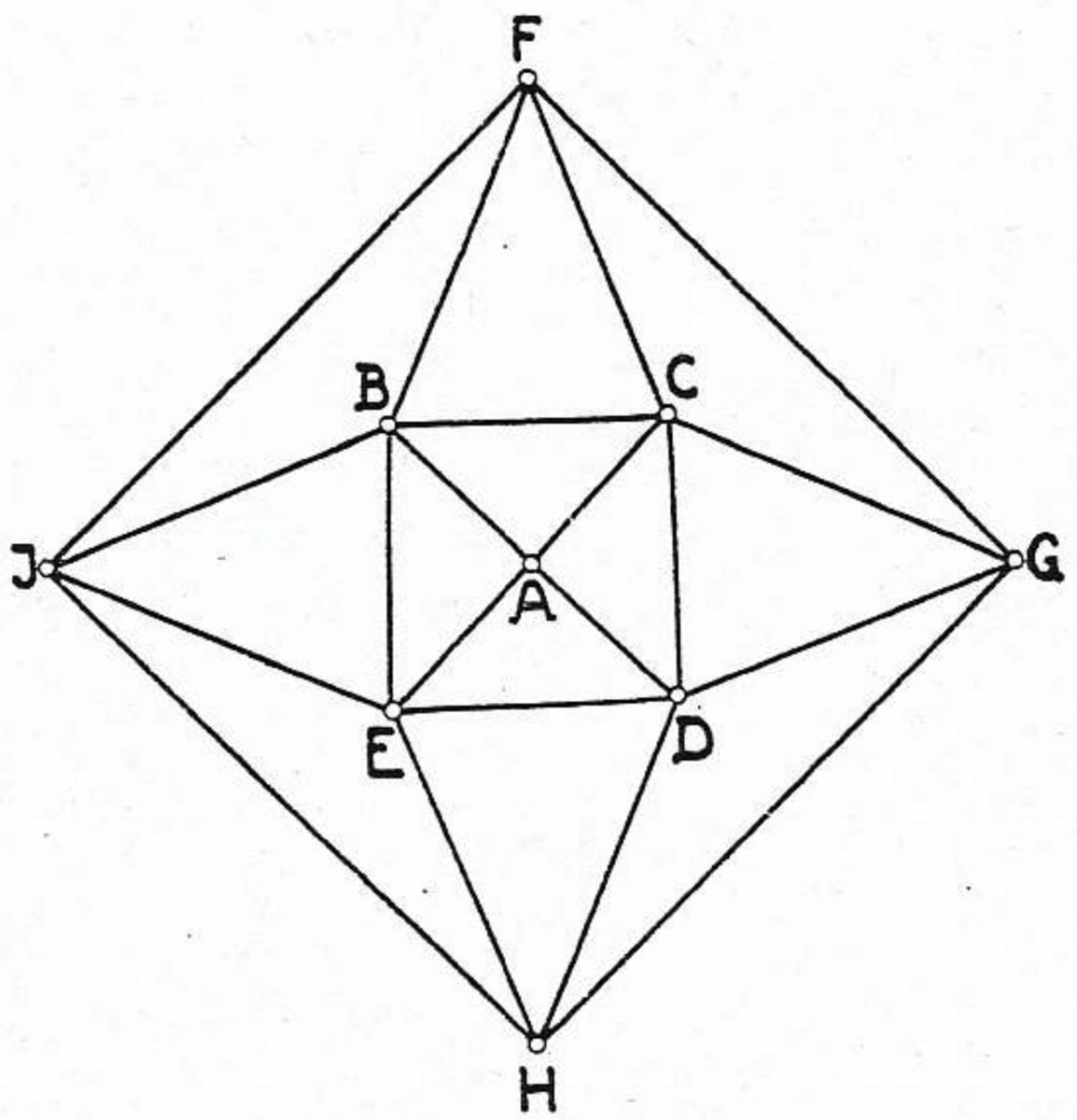
ここで,〔$BC$, $CD$, $DE$, $EB$ とそれぞれ3角形をなす点として $F$, $G$, $H$, $I$ を定めるとき〕$I$ と $G$ および $F$ と $H$ はそれぞれ一致してはならない.なぜなら,もし一致すると6次の頂点が現れるからである.したがって,さらに先へ進むことによって,外側の点 $F$, $G$, $H$, $I$ をそれぞれ5次の頂点にしなければならない.そのためには,外側の各辺上に3角形を置き,互いに向けて倒すという操作を続けることで,どの〔隣接する〕2つの3角形も上向きの辺を共有し,1番上の頂点が1点 $K$ で集まるようにするしかない.しかし,このときの $K$ は4次の頂点となるので,1)の場合ではなく2)の場合に該当する.ゆえに,18面体(1の場合)は不可能である.
この議論によって,〔$F$, $G$, $H$, $I$ が5次の頂点である場合に〕唯一可能なのは16面体(2の場合)であることもわかった.16面体は次のように構成できる.平行な平面上に,互いに $45^\circ$ だけ回転している2つの合同な正方形があり,近くの頂点どうしが正方形の辺と同じ長さの線分で結ばれている(図4).そして,それぞれの正方形上に,縦に伸びる辺が他の辺と同じ長さとなるように角錐を置けばよい.
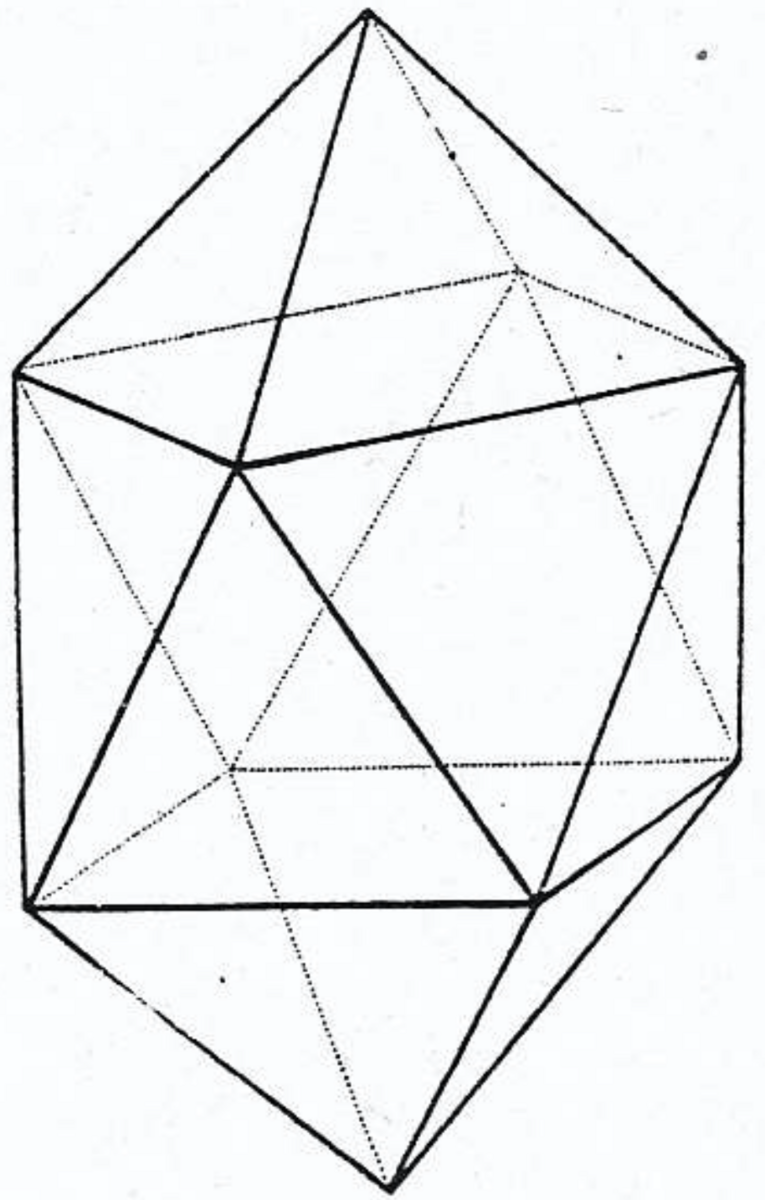
〔$F$, $G$, $H$, $I$ が5次の頂点とは限らない場合に〕図3を多面体にする方法はもう1つある.すなわち,空間的な4角形 $FGHI$ を2つの3角形(たとえば3角形 $FGI$ と3角形 $HGI$ )によって閉じることである.この方法によって次のような立体が得られる.3角柱を正方形の面が上向きになるようにとる.それぞれの正方形に,辺が等しい角錐を置く(図5).このようにして凸14面体が得られる.
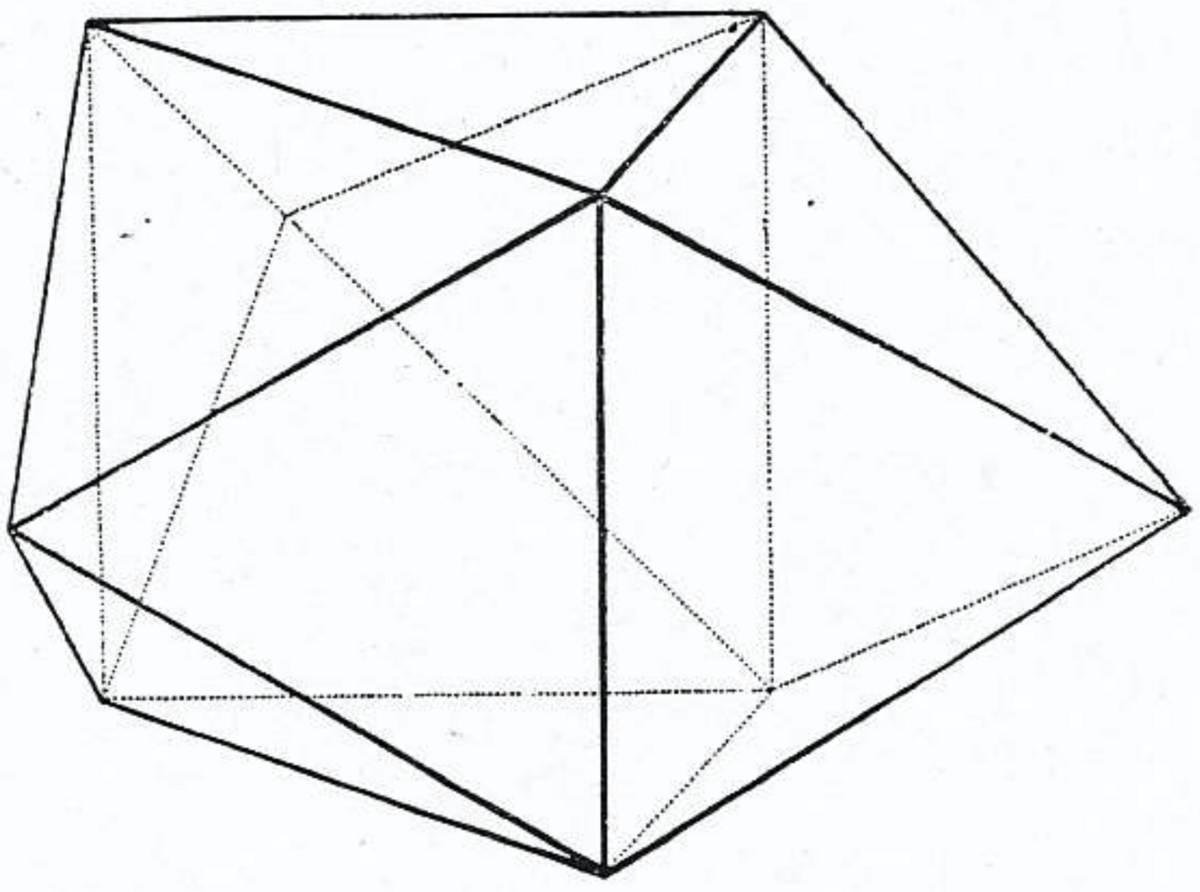
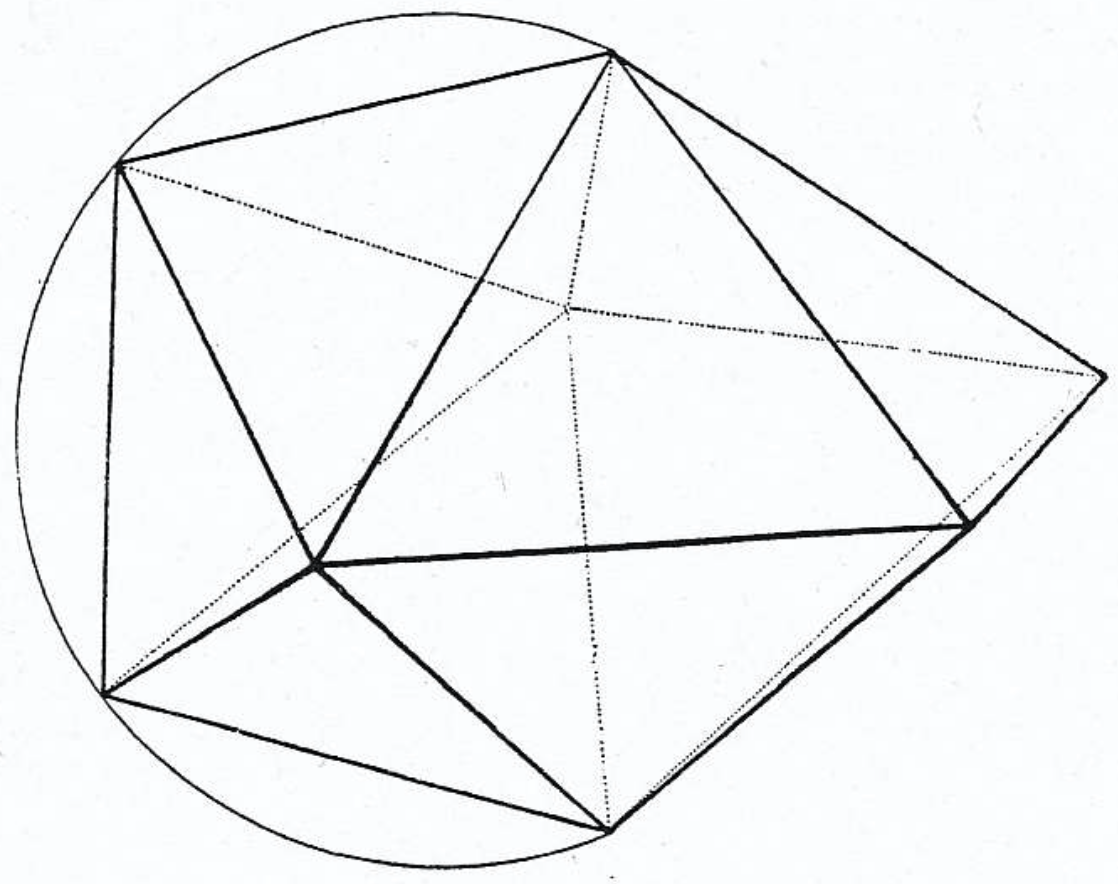
これによって,図3で与えられるあらゆる可能性が出尽くした.つまり,4次の頂点の周りに5次の頂点だけが並ぶ場合は,すべて考察し終えたことになる.そのため,あとは4次の頂点 $B$, $C$ が隣接している場合を考えればよい.このとき,$B$ の周りには4点 $A$, $E$, $C$, $F$ があり,$C$ の周りには4点 $B$, $E$, $D$, $F$ がある(図6参照).4点 $A$, $B$, $C$, $D$ はすべて $E$ からの距離が等しいので,$E$ を中心とする球面上にあり,〔同様に〕$F$ を中心とする球面上にもあるので,この2つの球面の交円上にある.そのため,図形 $ABCD$ はこの円を含む平面上での等脚台形となり(図7),点 $E$, $F$ はそれぞれこの円の中心 $M$ の鉛直上下方向に存在する(図8).
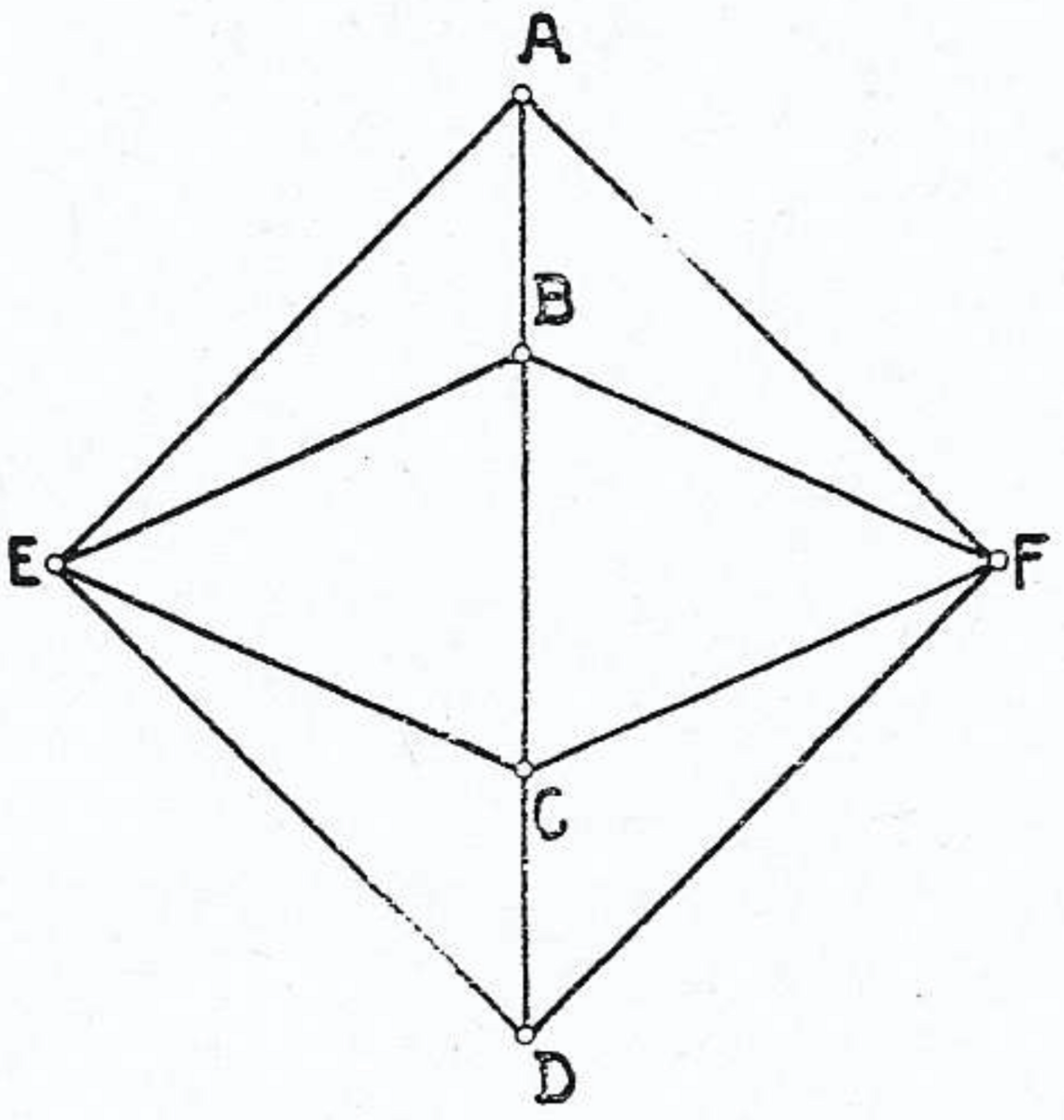
ここでまず,$A$ がまた4次の頂点であると仮定する.このとき,この円を含む平面において,先ほどと同様の議論によって,$D$ と一致する可能性のある5つ目の点が描けるので,この円には4角形か5角形が内接している〔$A$ と $D$ が一致することはない.もし一致すると $E$ や $F$ が3次の頂点になり,$a_3=0$ に反する〕.$E$ も $F$ もこの〔退化する場合も含めた〕5角形の辺と〔それぞれの場合で〕4つか5つの3角形をつくるので,8面体か図2の10面体のどちらかが得られる.
同様の議論が $D$ が4次の頂点である場合にも自然に成り立つ.ここで,$A$ と $D$ がどちらも5次の頂点であると仮定する.
$E$ が4次の頂点であると仮定する.このとき,$E$ を中心とする3角形の輪を完成させるために,3角形 $EAD$ を付け足す必要がある.ここで3角形 $ADF$ も正3角形であるが,この立体の面にはならない〔面になると $A$ も $D$ も4次の頂点になってしまうから〕.いま3角形 $ADF$ が欠けた8面体が得られた.この3角形のそれぞれの辺上には,5次の頂点 $A$, $D$, $F$ をそれぞれ中心とする〔3角形の〕輪を完成させるために3角形をもう1つずつ置く必要があり,これら3つの3角形をつなげる際にその頂点が一致するようにしなければならない.したがって,この頂点は3次の頂点となり,この立体は4面体の付いた8面体になる.この場合については,すでに議論したとおりである.
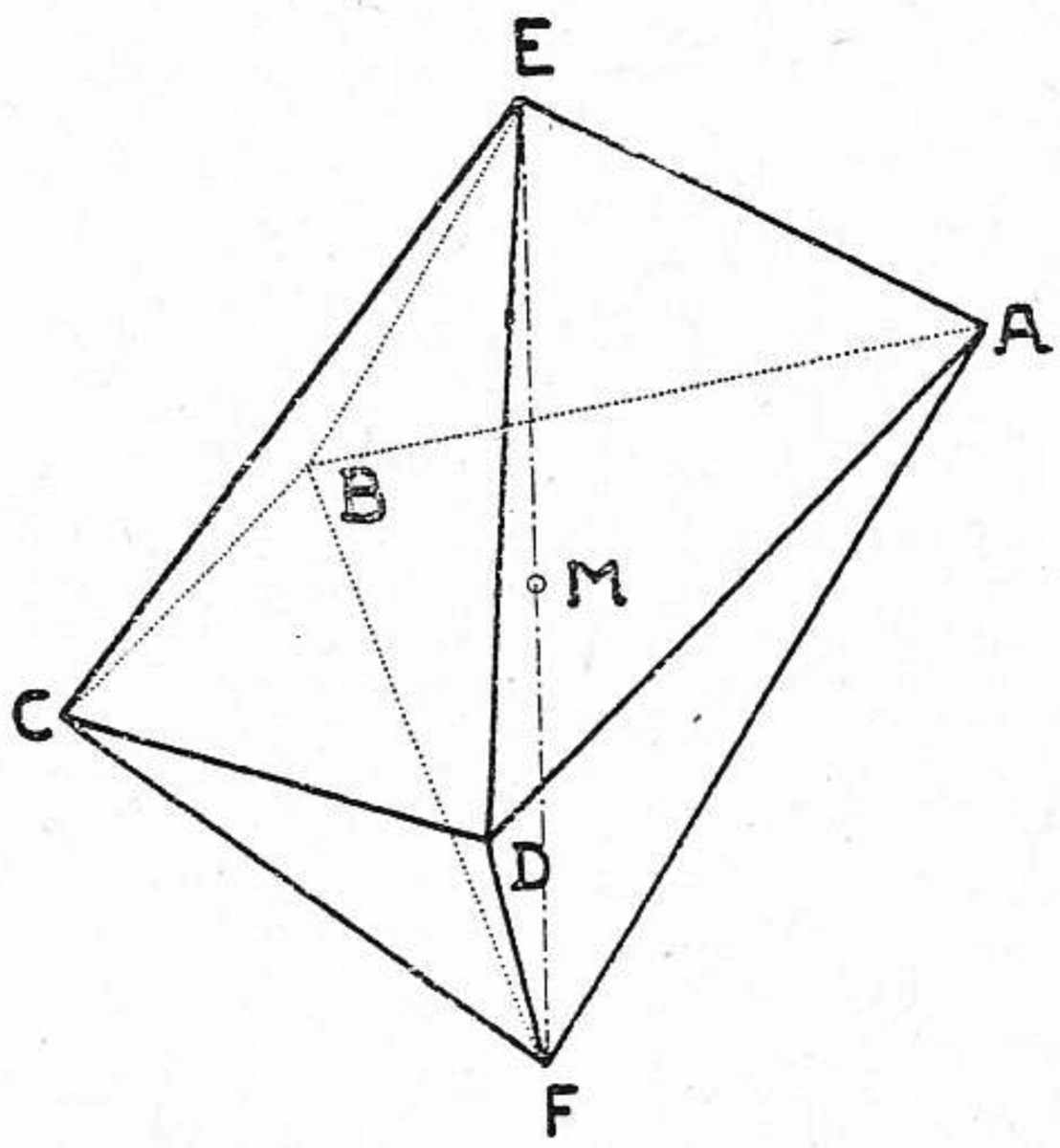
そのため,〔同様の議論が $F$ が4次の頂点である場合にも成り立つので〕$E$ と $F$ も5次の頂点であると仮定する必要がある.したがって,それぞれから5つ目の線分が伸びている.これらの線分が $G$ と $H$ で止まるとしよう(図9).このとき,$EA$ と $ED$ にそれぞれ3角形 $EAG$ と $EDG$ を付ける必要があり,同様に $FA$ と $FD$ にそれぞれ3角形 $FAH$ と $FDH$ を付ける必要がある.$G$ と $H$ は一致しない.もし一致すると,$A$ が4次の頂点になってしまうからである.いま $A$ を中心とする〔3角形の〕輪は3角形 $AGH$ によって完成され,$D$ を中心とする〔3角形の〕輪は3角形 $DGH$ によって完成される.ゆえに,隣接する頂点 $G$, $H$ は4次の頂点になる.そのため,$G$ または $H$ を頂点として含む3角形は,まさに図8に描かれているような2層の〔4角錐型の〕テントを形成している.この2層のテントは空間的な4角形 $AEDF$ と結合して12面体をともに形成しており,まるでシャム双生児*5のように融合しているので,これを「シャム12面体」と呼ぶことにする*6.
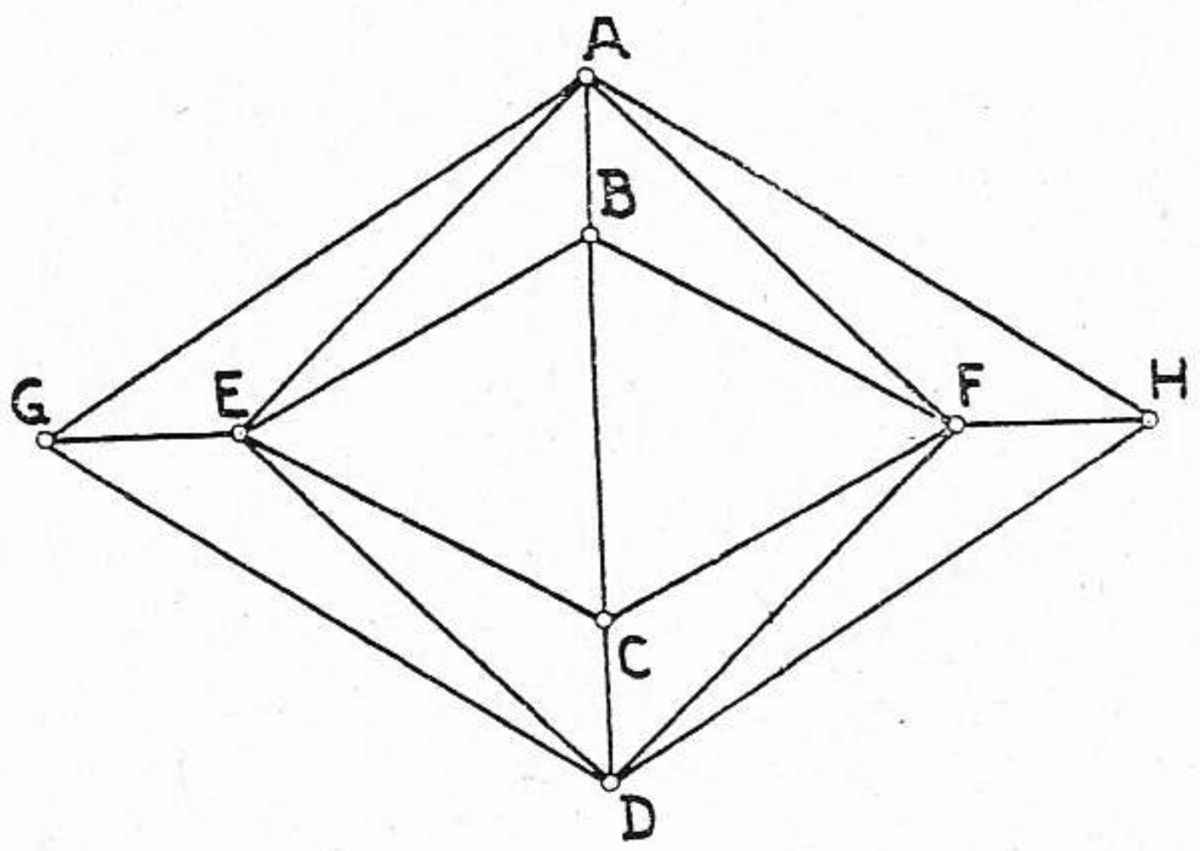
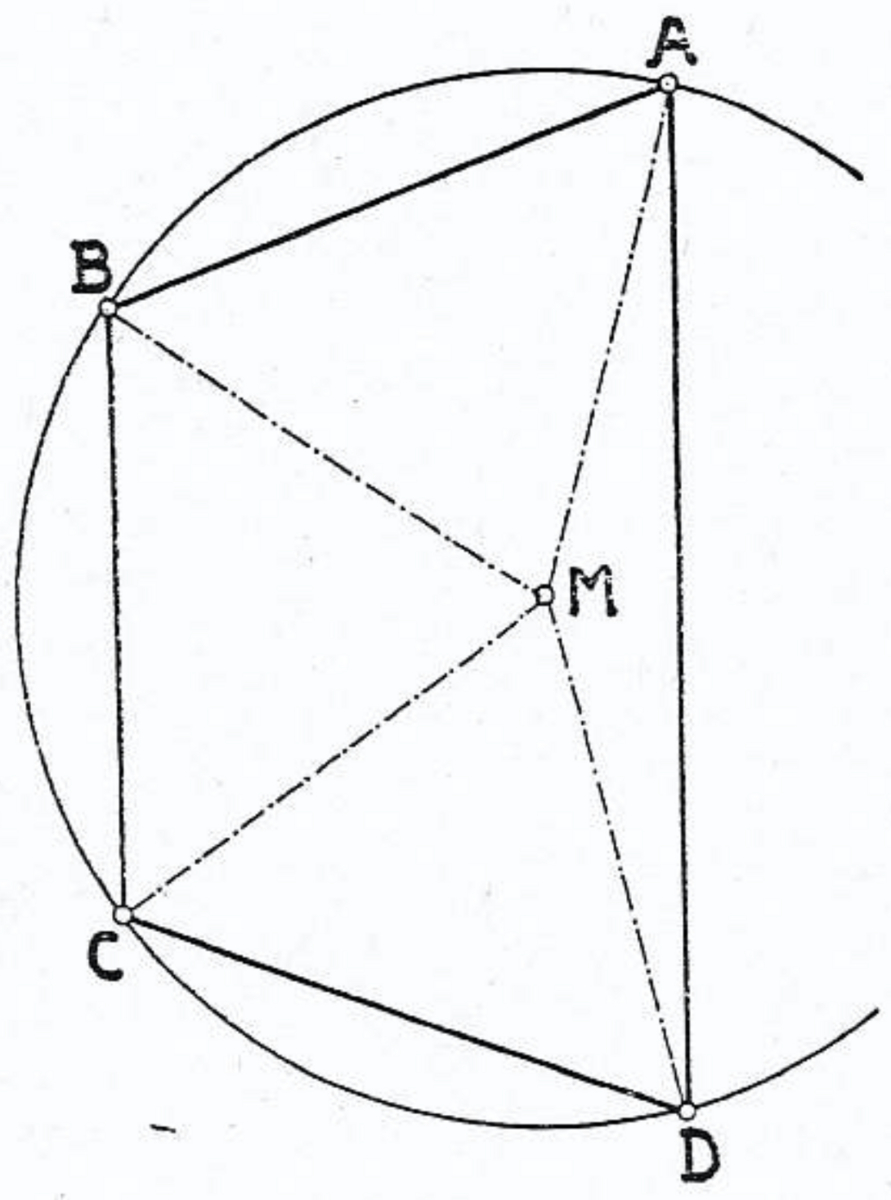
シャム12面体は次のように構成できる.台形(図7)の辺〔3つの等辺 $AB$, $BC$, $CD$ の長さ〕$a$ と外接円の半径 $r$ の比を,4つ目の辺 $AD$ が1層のテントの高さ $h$ 〔すなわち $EM$ の長さ〕の $2$ 倍に等しくなるように選ぶ.これが可能な理由は後述する.このため,空間的な4角形 $AEDF$ (図8)の対角線は長さが等しい.ここで,$DE$ と $AF$ の中点どうしを結ぶと,この4角形はその直線に関する回転移動によって自分自身にうつる.2層のテントはこの回転移動によって似た2層のテントにうつるので,最初の立体と合わせて,凸12面体が得られる.
比 $a:r$ を決定するために,$r=1$, $\angle AMB=2\varphi$ とおく(図7参照).このとき,次が得られる. \begin{align} a &= AB = 2 \sin \varphi, \notag \\ AD &= 2 \sin 3\varphi, \notag \\ h ^ 2 &= a ^ 2 - r ^ 2 = 4 \sin ^ 2 \varphi - 1. \notag \end{align} そのため,次の条件が得られる. $$4 \sin ^ 2 \varphi - 1 = \sin ^ 2 3\varphi.$$ ここで $\cos2\varphi=x$ と置くと,$\cos6\varphi=4x ^ 3-3x$ となるので,次が得られる. \begin{gather} 4(1 - x) - 2 = 1 - 4x ^ 3 + 3x, \notag \\ 4x ^ 3 - 7x + 1 = 0. \notag \end{gather}
この式は既約であり,実数解を3つもち,そのうちの1つは $-1$ から $+1$ までに存在する.すなわち, \begin{align} x &= \cos 2\varphi = 0.1445\dots, \notag \\ 2\varphi &= 80^\circ41'\dots \notag \end{align} である*7.
この $\varphi$ の値をもとにこの立体の正投影図*8を描くと,凸であることがわかる(図10).
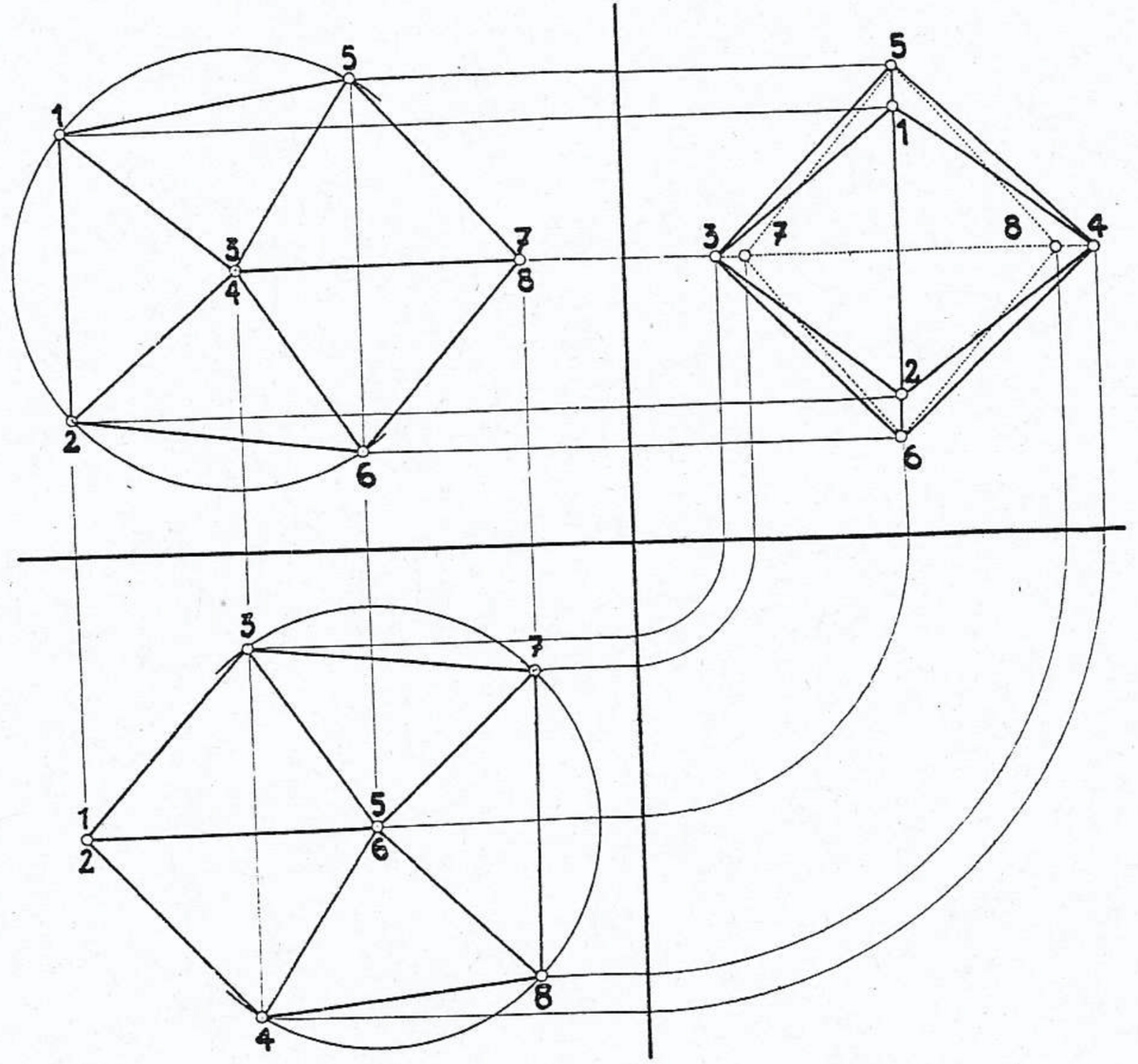
以下に斜投影図を示す.
コーシーの〔剛性〕定理によると,すべての凸多面体は剛性をもつ.すなわち,2つの多面体の面が合同でつながり方も同じならば,その多面体自体も合同である.したがって,これらの5つの立体は,正多面体のように,その形によって一意に決定される.
そのため,5つの正多面体に加えて,6面体・10面体・シャム12面体・14面体・16面体の5つの凸体も〔冒頭の〕ユークリッドの条件を満たしている.
*1:図版作成については,A. G. テナー氏に感謝する.
*2:(訳注)原文は2重引用符付きの“diëders”(英:dihedron)となっているが, 文字通りに読むと意味が通らないので,ここでは文脈を考えて「双角錐」(bipyramid, dipyramid)と訳し直した.
*3:(訳注)実際には切断面が新たに増えるので,面の数自体は3つではなく2つだけ減るが,ここでの議論には関係ない.
*4:(訳注)原文の“cosaëder”は“icosaëder”「20面体」の誤植である.
*5:(訳注)一般に一卵性双生児の分離不完全によって部分的に癒着ないし癒合している奇形を有する双生児を結合双生児と言う.シャム双生児とは結合双生児の古い俗称であり,19世紀にサーカスの見世物として欧米を巡業したチャン&エン・ブンカー兄弟の出身地がシャム(現在のタイ王国)であったことに由来する.
*6:(訳注)この呼称は明らかに不適切なので,現在では変形双5角錐やデルタ12面体と呼ぶ.
*7:(訳注)第1式の原文の “$\cos ^ 2\varphi$” は “$\cos 2\varphi$” の誤植である.
*8:(訳注)この投影図は第3角法ではなく第1角法で描かれている.