どうにも年を経るにつれて少しずつ思い出に綻びばかりが目立つようになるようなので、青春時代の良い思い出の大きな一つとして河合塾K会の数学科のカリキュラムを受講したときの感想でも書き記しておこうと思います。 www.kawai-juku.ac.jp
今は名称と現代数学のカリキュラムだけ変わったようですが、当時はMI・MII・MIII(X/Y)・MIV(X/Y)・MV(X/Y)という分け方になっていて、Xコースが現代数学でYコースが中高数学演習となっていました(要はポケットモンスターみたいなものだと言いたいところですが、私は残念ながらBW2世代なので、あまり言う資格がないかもしれません)。当時は『雪江整数1』を読んでいた頃だった気がするので、思い切ってMIからではなくMIIの途中から入会してしまい、その後にMIIIX以降のコースを受講していました。そういえば他にも、中高の同級生に影響されて情報科学を取っていましたが、今見ると三年制コースになっていて衝撃です。そうそう、情報科学科の先生とは、形式言語理論の学期の際に、黒田成幸氏についての議論をいくつか交わした気がします。今となっては言語学にばかり精を出しているので、何とも奇遇な運命だなとは感じます。
話を戻して、MIIコースは3学期しか取っていなかったので、あまり授業方針がよくわからないまま卒業してしまいましたが、当時は数研部員と一緒に線形代数のゼミを同時並行でやっていたので『代数4』はとても楽しかったですし、たしか『ランダウ・リフシッツ力学』も読み始めていたころだったので『解析4』でEuler-Lagrange方程式が出てくるのも面白かったです。
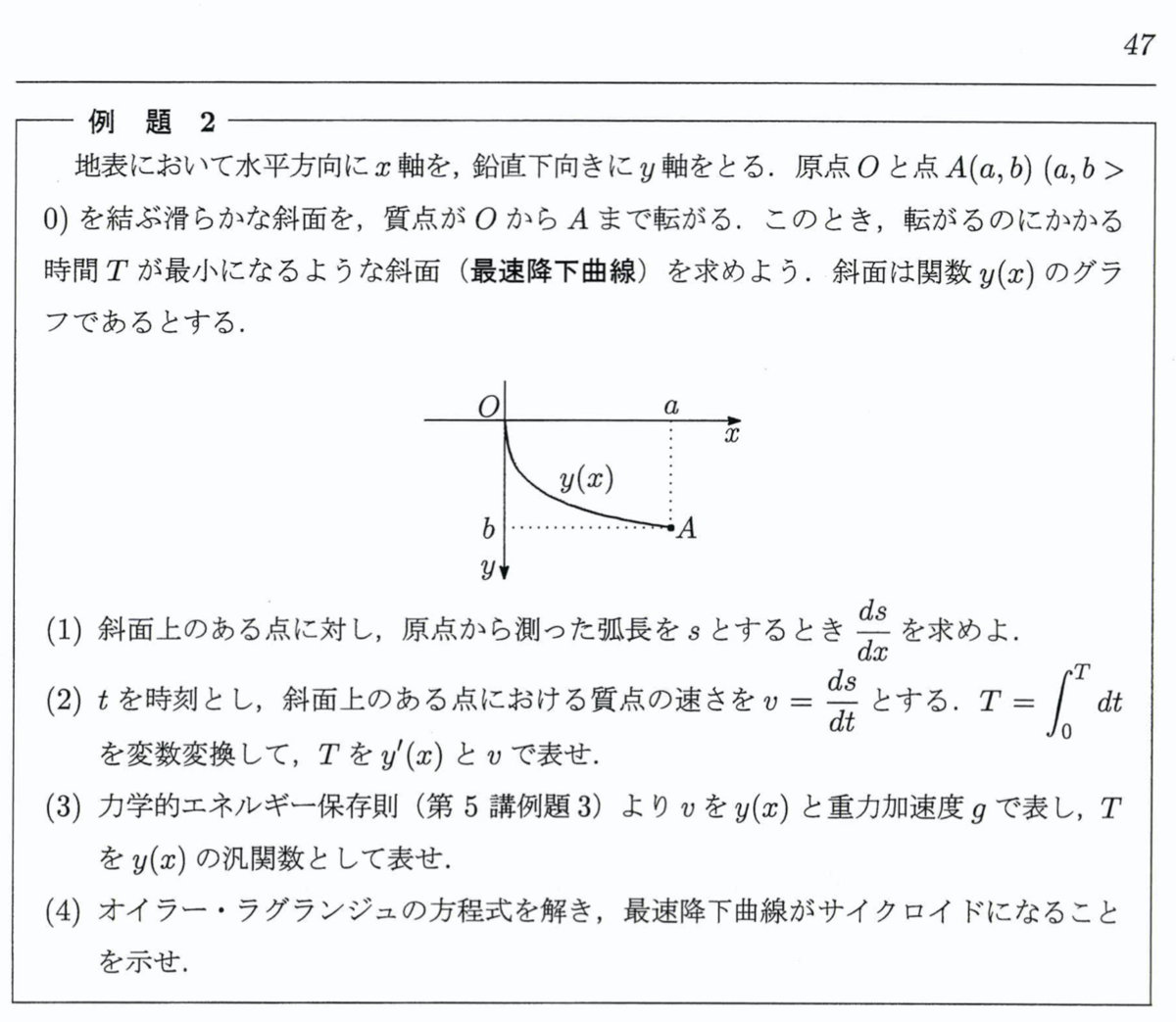
MIIIコースからは同級生が何人か一緒に受けるようになったので、とても充実した日々を過ごせていた気がします。Yコースに行く人もいましたが、Xコースにもたしか一人いたはずで、今も元気にやっているはずです。当時は不真面目な学生だったので復習プリントを全部解いて出していたわけではありませんでしたし、若かったので先生方にとことん教えを乞うということもできず、なんとか頑張って食らいつこうと必死になる生活が続いていたと記憶しています。『微分学』の先生とは全く交流はありませんでしたが、『代数入門』の先生とはいろいろな経緯があって今でもご指導を賜ることがあります。不肖の弟子未満だったかなと思いますが、それはそれとして面白い授業でした。これとかとても面白いですよね。
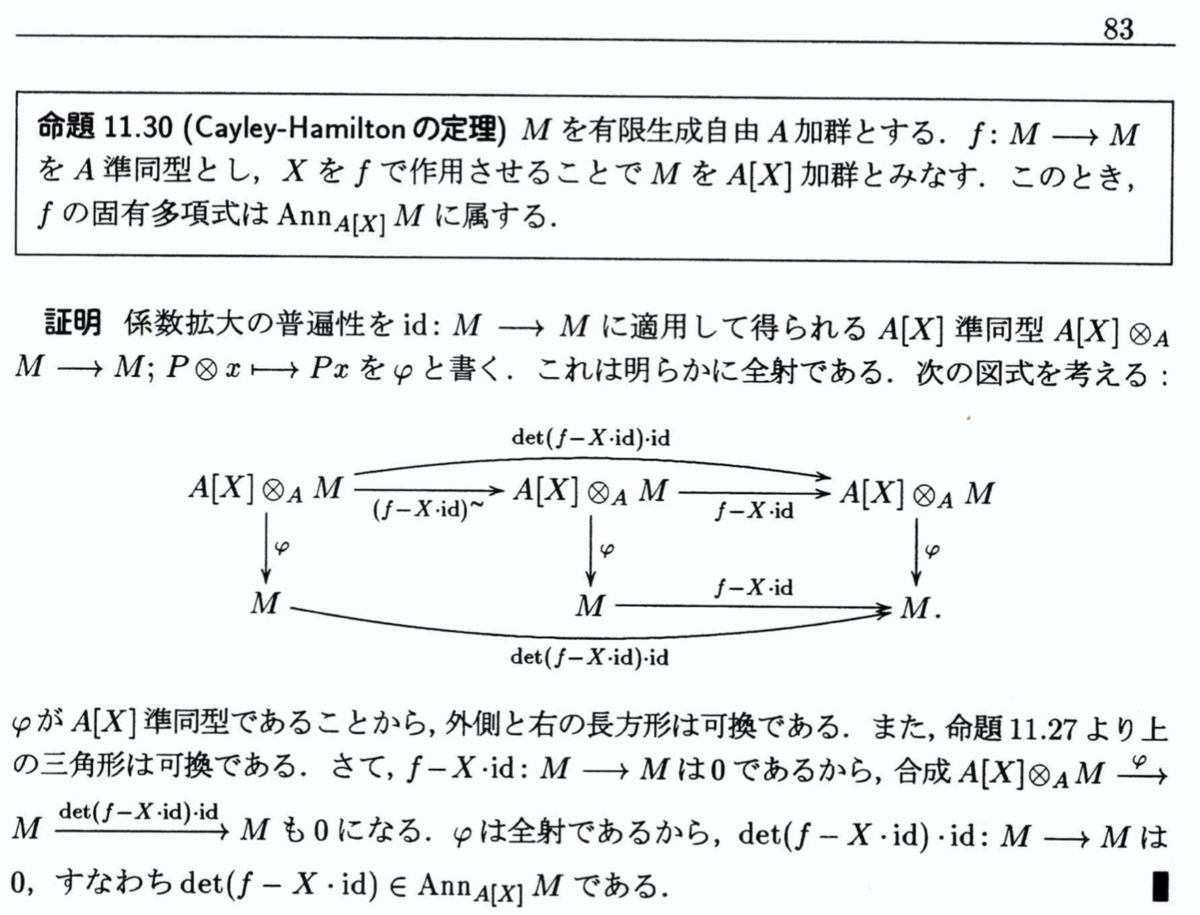
後期は『積分学』と『Galois理論』で、『積分学』にはそこまで辛い思い出はありませんが、『Galois理論』には非常に辛い思い出しかありません。最初の方は大丈夫でしたが、途中から大量の行間と記号の濫用が現れるので、とてもではないですが完全には理解しきれませんでした。特に今でも反省するべきだなと感じるのは、中高の部活が忙しかったので全部の講義には出きれなかったということです。講義や演習にはたくさん出た方がよいです! もしかしたら、この大学以降でも重要な教訓を認識させてくれるという点でも価値のある授業体験だったと言えるのかもしれません。
『Galois理論』での本質的な議論をまとめたのが、以下のPDFです。実は、もう今だからこそ時効なので言っていいとは思いますが、著者の @Asuka_Tsukimi さんは(まあ数年前のTwitter数学者界隈を知っている人なら誰でも知っているとは思いますが)当時とても有名な方で、私自身は『代数入門』と『Galois理論』の目次の画像がツイートされていたのをきっかけに入会したというわけです。このことを入会したばかりのときに事務局に話したら「よくわからないですが宣伝が上手くいっているんですねえ」と感心していましたが、まあ実際に入ったのは私ぐらいなので一般的な効果としてはどうなんだろうとは思いました。 asuka-math.amebaownd.com
また、三枝洋一先生の「Galois理論の証明」も参考になります。2001年頃のアーカイブで「講師紹介」を押してみると三枝先生の名前も出てくるので、おそらく何らかの形で執筆に関わっていらっしゃったのだろうと個人的に推測していますが……特に推測の域は出ません。そうそう、参考図書もとても味わい深い話が書かれていて、当時高校生だった私はあまりにも純情だったので数学に対する向学心をとても強く掻き立てられました。あれは、二度と決してあのような形では帰ってこないような熱気と神秘に満ち彩られた時代でした。
本テキストで紹介したGalois理論の圏論的定式化は、有名な数学者Grothendieckによって提唱されたものです。彼およびその協力者たちによって行われたセミナー(「マリーの森の代数幾何学セミナー」の一部)をまとめて文書化したものが[3]です。その内容は大変興味深く面白いものであり、筆者も数学を志した頃に夢中になって読んだものです。しかし、[3]のメインテーマは環、そしてスキームに対するGalois理論であるため、挑戦するのは今後の講座『スキーム論』を受講した後にするのがいいかもしれません。それまでに合わせてフランス語の基礎を勉強しておくとよいでしょう。Grothendieckの理論は[7]において解説されています。この記事はGalois理論の解説記事としても素晴らしいものであり、熱読すると得るところが多いでしょう。
……そしてやはり最も読んでいて安心できるのはブルバキ[1]の記述でしょう。「代数5」が体論に充てられています。筆者もこのテキストの執筆の際に何箇所か参考にしました。環論的な整理が行き届いている数少ない文献でもあるので、本講座の復習としても利用できます。なお、[2]の冒頭部は平坦性、忠実平坦性を扱っているので、本書と読み比べてみても面白いでしょう。
この「それまでに合わせてフランス語の基礎を勉強しておくとよいでしょう」という言葉を見て当時フランス語の勉強にも明け暮れていた気がしますが、授業前の空き時間に『新リュミエール』を解いていたら『微分学』の先生に「もしSGA1を読みたいだけならフランス語の詳しい文法を知る必要はないので、数学に集中して構いませんよ」と助言されたのも思い出しました。ここの時系列はいまいちよく思い出せませんが、高校の先生に『ハーツホーン』片手に相談しに行ったのもこのあたりだった気がします。当時相談させていただいた先生には今でもお世話になっていて、数少ない良い思い出の大きな一つを占めています。
フランス語と言えば、『被覆空間と基本群』を受けているときに délaçable というブルバキ由来(?)の用語が出てきて、一緒に受けていた一個下の同校生とTwitterで少しやりとりしていたのを思い出しました。被覆空間の絶対Galois理論やvan Kampenの定理に差し掛かったときには、二人で面白かったと言い合っていた気がします。次の記事も参考になりますが、単に unloopable と訳されています。 asuka-math.amebaownd.com
少し話を戻して、MIVXコースの前期は『複素解析学』と『多様体論』でしたが、正直な話をすると、MIIIXコースの微分積分学に比べても複素解析学は本当につまらなかったです。後期は『代数的整数論』と『層とコホモロジー』でしたが、『代数的整数論』もつまらなかったです。MVXコースは『解析的整数論』と『微分幾何とコホモロジー』でしたが、『解析的整数論』もつまらなかったです。しかし、『多様体論』『層とコホモロジー』『微分幾何とコホモロジー』はどれも難しかったですが非常に面白かったです。先生もテキストに載っていない発展的な事項も積極的に話してくださり、『多様体論』では local on the base/source の話や、『層とコホモロジー』ではc柔軟層の話をいろいろと聞きました。そういえば、『微分幾何とコホモロジー』の導入はとても面白くて、ある親友は「完全に同じことを考えていたことがあるのでウケる」と言っていました。全体的な “イメージ” としては『今野微分幾何』を層と圏の言葉で書いたような感じと言えばよいのでしょうか?

このあたりで気付いたのですが、自分はやはり解析や数論がほぼ全く好きではなくて、代数はそれなりに好き、幾何はかなり好き、基礎論は非常に興味あり(ちなみにK会では基礎論や集合論に関する講座は一切存在しません)、という感じなのです。いや、そもそも(少なくとも通常の)数学が好きなのかも怪しいのかもしれない……と思うようになりました。というわけで数学者になる道は選びませんでしたが、数学科に足を踏み入れてしまう前にこの洞察にまで至ることができたのは、実はとても良いことだったかなと感じています。
巷では少し誤解されているようですが、K会の現代数学コースの良さは、数学を専攻しない人間でも現代数学の美しさに触れられるという点にあると思います。これは中島さち子さんが次のように述懐している通りです(-K会講師OB・OG講師によるコラム- 数学つれづれ草 2015年度 | K会講師OB・OGによるコラム | K会 | 数学・情報科学・物理を深く学べる塾 河合塾)。
私が高校3年の頃、当時東京大学の学生だった吉田輝義さんが『輝義ゼミ』を開始しました。数学の名著を輪読していくゼミで、私はセーラー服のまま高校の帰りに参加させていただきました。そして輝義さんは「現代数学のような素敵で面白い人類の財産を、数学者だけのものにするのは勿体ない!」「僕たちもこんな場所が欲しかった」という熱い思いを河合塾の方にぶつけ、仲間と共にK会を立ち上げました。吉田輝義さんが「整数論」、伊藤哲史さんが「幾何学」、永井保成さんが「代数幾何学」、勝良健史さんが「解析学」等を担当し、それから怒涛のごとくカリキュラム作りやテキスト執筆が始まりました。
この執筆陣からも見てとれるように、少なくとも当時のK会は東京大学を中心とするアカデミズムと強い関係性があったらしく、かつてのK会なんでもセミナーの存在(これは高校時代の恩師を含む30代前後の数学界隈では有名なものらしいですが、私は卒業後に初めて知りました)や、東大数理の院生室にK会のテキストが置いてあること(これは最近どなたかの先生から伺った気がします)などからもそのことは窺えると思います。数理の翼に参加したときにも、夕食中になぜか代数幾何の先生方がK会『スキーム論』の話題を出していたのを覚えていますが、その文脈はすっかり忘れてしまいました。そういえば、なんでもセミナーについては、カピバラ先生も直近の記事で言及なさっていました。
この情報オリンピックメダリストの数学者が学生時代に初回の発表者になったのが2000年からはじまった「なんでもセミナー」です。当初は、代々木のK会でやっていたと記憶しています。 http://new.pya.jp/nandemo/ そして、2004年から「情報科学なんでもセミナー」がはじまります。 http://www.cs.toronto.edu/~kawamura/nandemo/old.html
なんでもセミナーは、レトロニムとして(情報科学のほうと区別するために)数学なんでもセミナーと呼ばれることがありました。数学なんでもセミナーは情報オリンピックのメダリスト、情報科学なんでもセミナーは数学オリンピックのメダリストが第一回発表者なのがちょっと面白いですね。この余談が挟まったのは、この時代のプログラムが書ける人たちは、他の分野にも興味を持って、広く交流を持っているのが普通であったという話をしたかったからです。
ここで衝撃的なのは「代々木のK会」という私たちの世代からすると一見意味のわからない表現が出てくることなのですが、生徒時代に事務局の方と雑談していたら「昔は新宿や代々木の近くにあったんですよ」と言われたことがあります。先生の中には「当時は筑駒を代表とする中高生を呼びやすい立地だったけど、本郷にはなかなか桜蔭ぐらいしか近い学校がないからね……」と仰る方もいた気がします(私の出席率があまり芳しくなかったのも、正直なところ少し遠かったからという面があります)。
あとは思い出せることが特になくなったので、一旦筆を置いておきます。
追記 (20231021): 葛西佑美 (2017)『東大医学部生が教える:本当に頭がいい人の勉強法』の第4章にある「K会(中高生に現代数学を教える塾)で学んだことなど」という節(217ページ〜218ページ)には、次のような記述が見られます。
K会の数学講座の1年目と2年目のクラスは高校数学の内容です。
私は高校数学については、自分で勉強を進めていたこともあって、中学2年の夏から2年目のクラスに入会しました。
そのときの講座は代数と幾何と解析でしたが、普通の高校生用の参考書にないような外積、線形変換、固有値、固有ベクトル、リーマン和、などをやっていてボルツァーノ・ワイエルシュトラウスの定理、ニュートン法なども扱っていました。
そのときの自分にちょうどいいレベルだったので、このタイミングで入会して正解だと思いました。
質点の力学のような物理分野も、少し含まれていました。
これはMIIコースの2学期『幾何4』『解析3』と3学期『代数4』『解析4』の内容です。
中3からはいよいよ現代数学コースに入りました。
代数学(環や群の性質を学び考え方や言葉の使い方を学べました)、微分学(コンパクト性、ノルム空間、Lipschitz連続性も勉強しました)、積分学(速度〔測度の誤字〕の構成、Lebesgue速度〔測度の誤字〕、Fubiniの定理、変数変換公式も学べました)など大学の数学科で学ぶ内容の基礎的な部分を学びました。
これは旧MIIIXコースの内容です。
高1からは代数的整数論、層とコホモロジー、解析的整数論、デアル類群〔イデアル類群の誤字〕の有限性、ゼータ関数〔、の抜け〕有限群の表現論、楕円曲線、Lie群とLie環、コンパクトRiemann面、
これは旧MIVXコースの内容だけでなく、講習の『有限群の表現論』『楕円曲線1, 2』『Lie群とLie環』『コンパクトRiemann面』を含めて、さらになぜか旧MVXコースの『解析的整数論』となぜかその「イデアル類群の有限性」と「ゼータ関数」という章を同列に並べたものです。
高2からは付値体と $p$ 進体、de Rhamコホモロジー、アフィンスキーム……
de Rhamコホモロジーとアフィンスキームはそれぞれ旧MVXコースの『微分幾何とコホモロジー』と『スキーム論』での内容であり、「付値体と $p$ 進体」は旧MIVXコースの『代数的整数論』での付値環と $\mathfrak{p}$ 進付値を指しているように思われます。
列挙して気づきましたが、何がなんだかわからないですね。とにかくとてもとても難しくて、わかったような気がする状態でした。でもなんだか楽しかったです。最近は数学に触れていないので、このあたりの内容は記憶が薄れています。
上述されている受講の順番に少し疑問点が残るのは、おそらく記憶が薄れているからかもしれません。もちろん、カリキュラムの改訂があった可能性もありますが、自分にはあまりそういう記憶はありませんでした。
カリキュラムでは高2の3学期に引退して、受験勉強に向かえるよう配慮があるのですが、私はもっと現代数学を勉強したくて、高3もしばらく通わせていただきました。
正規のテキスト自体は1学期〜2学期ぐらいで終わるようになっていて、3学期は在籍している講師の専攻に応じてテキストを使い分けるという感じだった気がします。
K会の本棚には有名な数学書がずらりと並んでいて、いつでも借りることができます。教室でも家でも、数学の世界にどっぷりつかることができる楽しい空間になっています。
当時通っていたK会の教室は事務局と講師室と本棚が一体になっていたので、事務局や先生方とお話をしながら『ブルバキ数学原論』などを借りることができたのを思い出しました。加藤文元先生おすすめの『代数2』を読もうとして、高1の頃に借りていたのも今となっては懐かしいです。
なんだかんだ言って、私が思うに最高の線形代数の教科書は、やっぱりブルバキの「代数2」だと思う。多分、ブルバキの中でも、傑作のひとつだろうと思う。
— Fumiharu Kato 加藤文元(Bungen) (@FumiharuKato) 2018年7月3日