注意書き
清史弘 (2003) を読み終えたのですが, 解の配置は割と多くの参考書でも確立されているようなことが多かったのに対し, 2.4 「ノミネート方式」についてはネット上でも情報がほぼ見当たらない上に, 現在出版されている 清史弘 (2016) の p. 114 にしか (筆者が記憶している限りでは) その残り香が見当たりませんでした. せっかく実りの多い手法なのに知名度が低いどころか口頭伝承レベルにまでなっていてはもったいないと思ったため, 同書よりも理論的にまとめておきます (演習問題や具体的な説明の量は同書の方が断然豊富なので手を動かしてみたい人はそちらをどうぞ). また, 本来ならば考案者に敬意を表して「ノミネート方式」とすべきでしょうが, 2.3.1「予選決勝法」との親和性とその語呂の良さから「ノミネート法」と呼ぶことにします.
一般論
ノミネート法とは, とくに $2$ 変数以下・$2$ 次以下の関数のある範囲における最大・最小問題に対し, 安直に場合分けするのではなく「最大・最小値をとる候補をノミネートして調べる」という発想に基づいた手法を指します.
候補の候補
次の命題が基本的です:
命題1.
$[a,b]$ で連続な関数 $f(x)$ の最大 (小) 値を与える $x$ は, (1) 両端, (2) 極大 (小) 値を与える $x$ のいずれかである.
証明.
$(a,b)$ 内にある極大 (小) 値を与えない点 $x$ は, その近傍に $f(x)$ より大きい (小さい) 値をとる点が存在するから.
処理方法
原理的に次の2つに帰着します.
命題2.
$$\begin{aligned}
\max\{a,b\} \leq c &\iff a\leq c \land b\leq c \\
\max\{a,b\} \geq c &\iff a\geq c \lor b\geq c \\
\min\{a,b\} \leq c &\iff a\leq c \lor b\leq c \\
\min\{a,b\} \geq c &\iff a\geq c \land b\geq c
\end{aligned}$$
命題3.
$[a,b]$ で連続な関数 $f(x)$, $g(x)$ に対し
$$\begin{aligned}
\max_{a\leq x\leq b}\{\max\{f(x),g(x)\}\} &=\max\{\max_{a\leq x\leq b}f(x),\max_{a\leq x\leq b}g(x)\} \\
\min_{a\leq x\leq b}\{\min\{f(x),g(x)\}\} &=\min\{\min_{a\leq x\leq b}f(x),\min_{a\leq x\leq b}g(x)\}
\end{aligned}$$
注意.
$\min\max$ や $\max\min$ についてこのような言い換えはできない.
各論
なんとたったこれだけでノミネート法のお膳立てが済んでしまいました. ではどのように用いていくのか紹介していきましょう.
$1$ 次関数
問題4.
「すべての正数 $b$ について $|ax+b|\geq1$ かつ $0\leq x\leq 1$ を満たす $x$ が存在する」ための $a$ の条件を求めよ.
解答.
$|ax+b|$ $(0\leq x\leq 1)$ は単調なので最大値は端点 $x=0,1$ のどちらかで実現されるから, すべての正数 $b$ について $|b|\geq1$ または $|a+b|\geq1$ が成り立つことが必要十分. $b\geq1$ では $a$ によらず成立し, $0 < b < 1$ では $|b+a|\geq1$ すなわち $b\geq -a+1$ または $b\leq -a-1$ が成り立つことが必要十分で, それは $-a+1\leq 0$ または $-a-1\geq1$ すなわち $a\geq1$ または $a\leq -2$ と同値であり, これが求める $a$ の条件である.
$2$ 次関数
もし $x ^ 2$ の係数が正ならそのグラフは下に凸である区間における最大値は必ず両端の値で取ることがわかります. というわけでたとえば区間 $[a,a+2]$ において最大値がどうこうという問題は必ず $f(a)$ と $f(a+2)$ を見るだけで済んでしまうというわけです. これはかなり嬉しいので手頃な問題で使ってみると威力が分かるでしょう.
極値がある場合
問題5.
$[a,b]$ で連続な関数 $f(x)$ がある $c\in(a,b)$ に対し $f'(c)=0$ となるとき, (1) $f(x)$ がつねに $0$ 以上になる条件と (2) 少なくとも $1$ つは $f(x)\leq 0$ となる $x$ が存在する条件を求めよ.
解答.
(1) $\min f(x) \geq 0$ すなわち $f(a) \geq 0$ かつ $f(b) \geq 0$ かつ $f(c) \geq 0$.
(2) $\min f(x) \leq 0$ すなわち $f(a) \leq 0$ または $f(b) \leq 0$ または $f(c) \leq 0$.
というわけでたとえば $2$ 次関数の場合は「極値をもつか否か」という場合分けをすればかなりスッキリ解答できます. その際は単純に微分して解を求めて (もし $x ^ 2$ の係数にもパラメータがあればその場合分けも適宜して) どうのこうのとすればよいです.
$2$ 変数の場合
一般的には「予選決勝法*1→ノミネート法」とすればよいです. そうでないケースもおおよそ少し工夫すればこの発想に近くなることがほとんどです.
問題6. (2000年 東大文系 第2問)
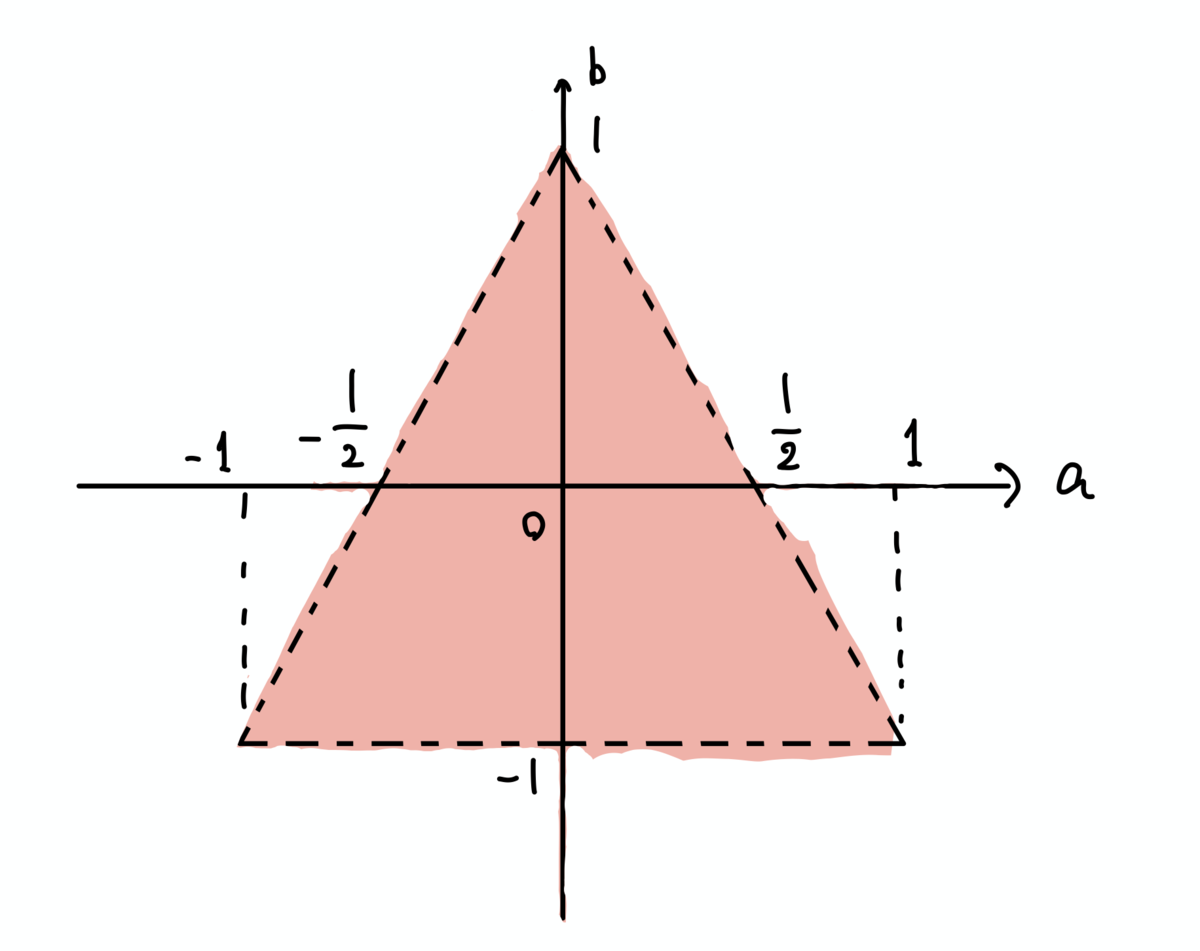
$xy$ 平面内の領域 $-1\leq x\leq 1$, $-1\leq y\leq 1$ において $f(x,y)=1-ax-by-axy$ の最小値が正となるような定数 $a$, $b$ を座標とする点 $(a,b)$ の範囲を図示せよ.
解答.
$y$ を固定し $m(y)\coloneqq\displaystyle\min_{-1\leq x\leq 1}f(x,y)$ とおく. このとき $f(x,y)=-(a+ay)x+1-by$ は $x$ の高々 $1$ 次関数なので最小値は区間の端の少なくともいずれかで実現し, すなわち $$m(y)\coloneqq\displaystyle\min_{-1\leq y\leq 1}\{f(-1,y),f(1,y)\}$$ であるが,
$$\begin{aligned}
f(-1,y)&=(a-b)y+a+1\\
f(1,y)&=-(a+b)y-a+1
\end{aligned}$$
はいずれも $y$ の高々 $1$ 次関数なので最小値は区間の端の少なくともいずれかで実現し, したがって
$$\displaystyle\min_{-1\leq x,y\leq 1}f(x,y)=\min_{-1\leq y\leq 1}m(y)=\min\{f(-1,-1),f(-1,1),f(1,-1),f(1,1)\}$$
となるから, $f(-1,-1)$, $f(-1,1)$, $f(1,-1)$, $f(1,1)$ がすべて正となる, すなわち $b>-1$ かつ $b<2a+1$ かつ $b<-2a+1$ が求める範囲を与える.
参考文献
清史弘. (2003). 「受験数学と教えられない数学」. 『数学・受験教科書』, 12. SEG出版.
清史弘. (2016). 『新数学 Plus Elite I・A』. 駿台文庫.
