『理論物理への道標』問題 1.1 (3) の解答には誤りがあります。
問題 1.1 地上から高さ $h_0$ のところから人が初速 $0$ で落下を開始し、高さが $\dfrac{1}{2}h_0$ になったとき、身につけていたパラシュートを開き、最後には、落下の速さが高さ $\dfrac{1}{2}h_0$ における速さに比べて十分小さく、ほぼ一定の値となって地上に達した。人とパラシュートの質量の和を $m$、また、落下の速さが $v$ のとき、開いたパラシュートの空気抵抗によって人にはたらく鉛直上向きの力を $kv$($k$ は正の比例定数)とする。空気抵抗はパラシュートを開いたときにだけはたらくと考えて、以下の設問に答えよ。ただし、重力加速度の大きさを $g$ とする。
(3) 人の鉛直下向きの速さ $v$ は落下時間 $t$ と共にどのように変化するか。
高さ $\dfrac{1}{2}h_0$ に到達するまでの落下時間は $t_0=\sqrt{\dfrac{h_0}{g}}$ なので、$0\leqq t\leqq t_0$ では速さが $0$ から $\sqrt{gh_0}$ まで線形に増加します。
$t\geqq t_0$ では、運動方程式が鉛直下向きを正として $m\dot{v}=-kv+mg$ なので $$v=\frac{mg}{k}+\left(\sqrt{gh_0}-\frac{mg}{k}\right)e^{-\frac{k}{m}(t-t_0)}$$ となり、$t\to\infty$ で $v\to\dfrac{mg}{k}$ という「ほぼ一定の値」になります。問題文には「落下の速さが高さ $\dfrac{1}{2}h_0$ における速さに比べて十分小さく」とあるので、$\dfrac{mg}{k}<\sqrt{gh_0}$ であることがわかります。
実際には $t_0\leqq t\leqq t_1$ で落下した距離が $\dfrac{1}{2}h_0$ となるような時刻 $t_1$ で地上に達することがわかりますが、それは
$$\begin{aligned} \dfrac{1}{2}h_0 &= \int_{t_0}^{t_1}\left(\frac{mg}{k}+\left(\sqrt{gh_0}-\frac{mg}{k}\right)e^{-\frac{k}{m}(t-t_0)}\right)dt \\ &= \frac{mg}{k}(t_1-t_0)-\frac{m}{k}\left(\sqrt{gh_0}-\frac{mg}{k}\right)(e^{-\frac{k}{m}(t_1-t_0)}-1) \end{aligned}$$
を解くことにより求められます。ここで、適切に変数を置換することにより、上の方程式は
$$aT=be ^ T+c$$
と変形できます。このような指数関数を含む超越方程式は $f(x)=xe ^ x$ の逆関数である Lambert の $W$ 関数 を用いて解くことができます(たとえば伊藤 (2019) が教育的な文献です)。
$$T=\frac{c-aW(-(b e ^ {c/a})/a)}{a}$$
これを数値計算するのは少し面倒ですが、グラフの概形そのものは以上の考察から簡単に書くことができます。
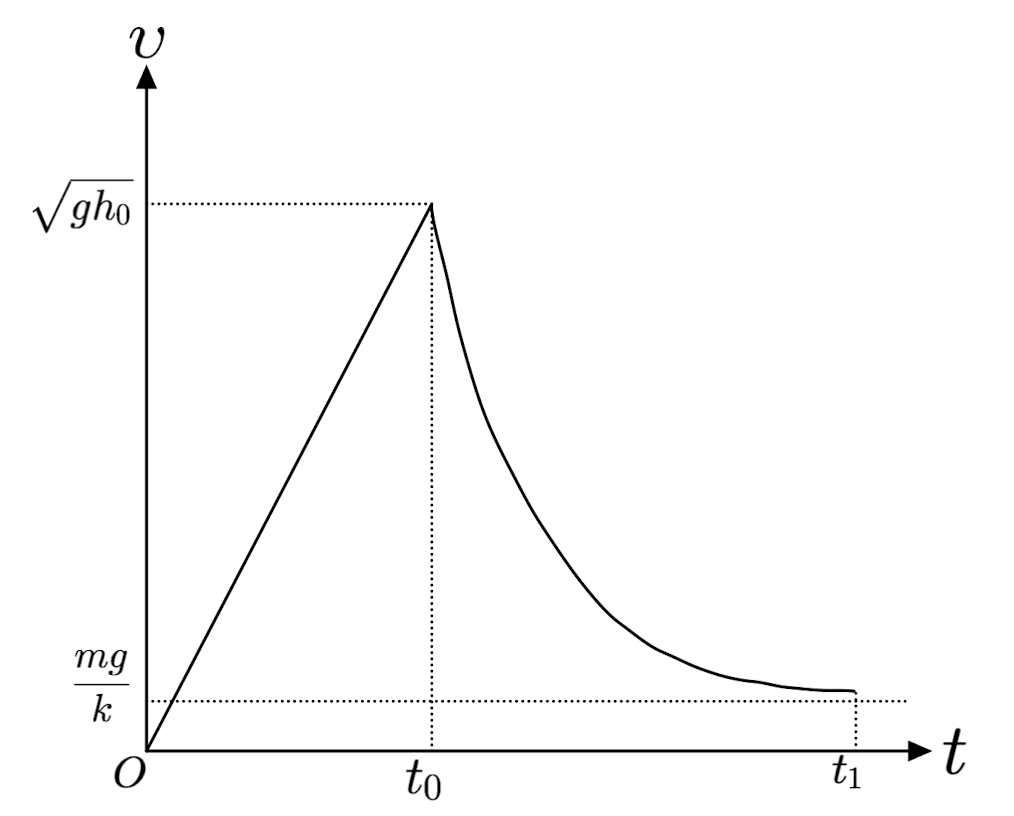
しかし本書の解答は次のようになっています。どう考えても $\dfrac{mg}{k}\approx0$ とは見なせないはずなので、これは不適切な概形であると言えます。
図 2
