同心ソレノイドの相互インダクタンスの相反定理

物理
本稿はまだ考察中のトピックを一旦整理するために書かれたメモ書きなので, 文体は全く整っておりません. 今後また何か進展があれば根本的な加筆修正を行います.
定理1. (相互インダクタンスの相反定理) 任意のコイル $C_i$ と $C_j$ に対して, その相互インダクタンス $M_{ij}$ と $M_{ji}$ は等しい.

これは次の定理から即座に従います.

定理2. (Neumann の公式) $$L_{ij}=\frac{\mu_0}{4\pi}\oint_{C_i}\oint_{C_j}\frac{d\bm{r}_i\cdot d\bm{r}_j}{|\bm{r}_i-\bm{r}_j|}$$
注意. Neumann の公式で自己誘導係数 $L_{ii}$ を求めようとすると積分が無限大に発散してしまうので, 導線の太さを有限にしておいて計算する必要があるが本稿では関係がないので割愛する.
証明. $C_i$ を貫く磁束は Stokes の定理により $$\Phi_i(t)=\int_{S_i}\bm{B}\cdot\bm{n}dS=\oint_{C_i}\bm{A}(\bm{r}_i)\cdot d\bm{r}_i=\frac{\mu_0}{4\pi}I_j\oint_{C_i}\oint_{C_j}\frac{d\bm{r}_i\cdot d\bm{r}_j}{|\bm{r}_i-\bm{r}_j|}$$ となるので示された.
注意. もしエネルギー $$U=\frac{1}{2}\sum _ {i,j}L _ {ij}I _ iI _ j=\frac{1}{2}\sum_{i}I_i\Phi_i$$ が（たとえば）$C ^ 2$ 級であることを仮定するのなら $$L_{i j}=\frac{\partial \Phi_{i}}{\partial I_{j}}=\frac{\partial}{\partial I_{j}} \frac{\partial U}{\partial I_{i}}=\frac{\partial}{\partial I_{i}} \frac{\partial U}{\partial I_{j}}=L_{j i}$$ とすることで簡単に示すことができる. これは熱力学の Maxwell の関係式と全く同じ事情である.

実は相互インダクタンスの相反定理はエネルギー保存則と深く結びついている. というのも $$\int\left(MI _ 1\frac{dI _ 2}{dt}+MI _ 2\frac{dI _ 1}{dt}\right)dt=MI _ 1I _ 2$$ のようにできるのは $M _ {ij}=M _ {ji}$ のおかげであり, これが成り立っていなければ保存するエネルギー量が定義できない.

さらに，オンサーガーの相反定理 (reciprocity theorem) から，エネルギー保存則が成り立つためには，$$L _ {12} = L _ {21} \tag{9.17}$$ が成り立たなくてはいけないことが知られている．(岩田 2020, p. 131)

実はこの定理が一見すると破れるように見える例があり, 本稿を執筆した理由はそこに由来しています. それが次のような同心ソレノイドです.

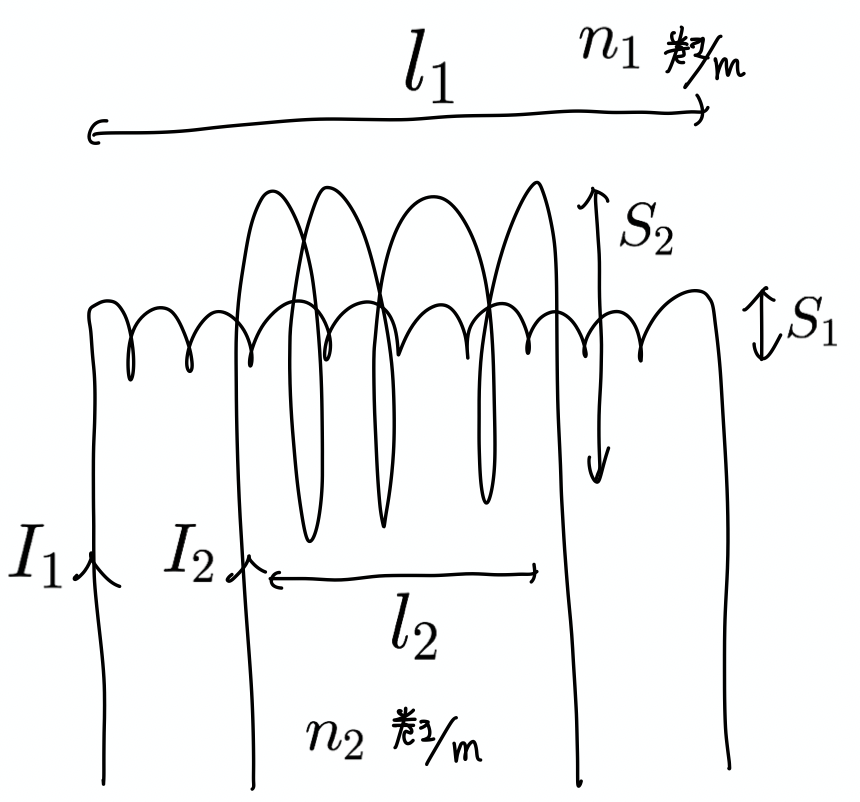
ところでソレノイドの磁場のでき方はよく学校の実験で砂鉄を置いて観察したことがあるはずです. それを考えると, 磁束はそれぞれ次のように計算できるはずです.

$$\begin{cases} {\Phi} _ {1}={\mu} _ {0}n _ 1 ^ 2S _ 1 l _ 1 I _ 1+{\mu} _ {0}n _ 1 n _ 2 S _ 1 l _ 1 I _ 2\\ {\Phi} _ {2}={\mu} _ {0} n _ 1 n _ 2 S _ 1 l _ 2 I _ 1 +{\mu} _ {0}n _ 2 ^ 2 S _ 2 l _ 2 I _ 2 \end{cases}$$

なんと $M _ {12}=\mu _ 0 n _ 1 n _ 2 S _ 1 l _ 1\neq\mu _ 0 n _ 1 n _ 2 S _ 1 l _ 2=M _ {21}$ となり相反性が崩れているように見えます.

事態をよく把握するために相反性が崩れない場合を考えてみましょう. まずソレノイドは無限長近似のもとで内部だけに一様磁場 $B=\mu_0 nI$ ができ外部には全く磁場を作らないということを確認しておきます. これは Ampère の法則から容易に導かれます.

  • $l_1=l_2$ であれば無限長近似の破綻が見えないので相反性は崩れません.
  • 鉄心などの強磁性体にコイルを巻きつけている場合, 磁束は磁気抵抗が極小の閉曲線を形成するので, 同心ソレノイドでさえあればコイルが重なっておらず分かれて巻きつけられていたとしても, どんなサイズであっても, ほとんどの磁束は鉄心の中を通り外部に出ていくことがない. したがって, 本質的には磁場を閉じ込めた長さが効いてくるのだが, たとえば $l_1$, $l_2$ を鉄心の長さ $l$ と置き換えて計算するのは第一近似として適切である. (ちなみに海外の講義録を見てみたら全部黙って $l$ に置き換えていた. そんなに自明なのか？) このことはトロコイドコイルでの計算とのアナロジーを考えると納得がいくし, 逆に受験で出てくるトランスがほぼ全部トロコイドなのは（工学上のデファクトスタンダードだからなのか知らないが物理的には）コイルを密結合にすることではなく, 他の回路との相互作用を防ぐために磁場を閉じ込めておくということなはず.

問題なのはやっぱり真空中の場合なのですが, 実は無限長近似に忠実に考えると「コイルの端面で磁場が消える」という描像を取るのが正しいと考えれば一気に相反性は満たされるのではないでしょうか？ なぜならコイル1を通る磁束のうち相互インダクタンスに関わる部分に長さの補正がかかるからです.

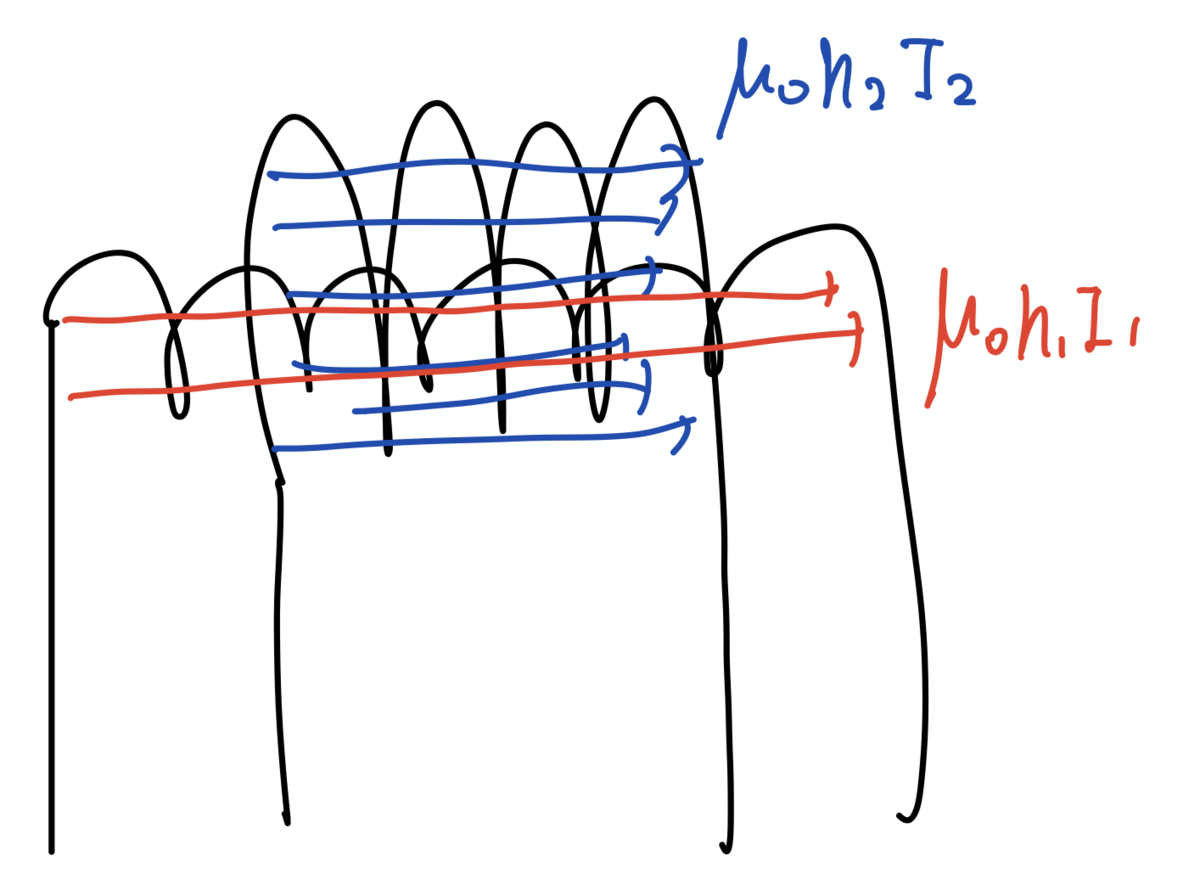
重なった同心ソレノイドは上と下の二つに完全に分類されるわけですが, どちらも無限長近似で想定される磁場のでき方からはこう考えるしかなさそうです.

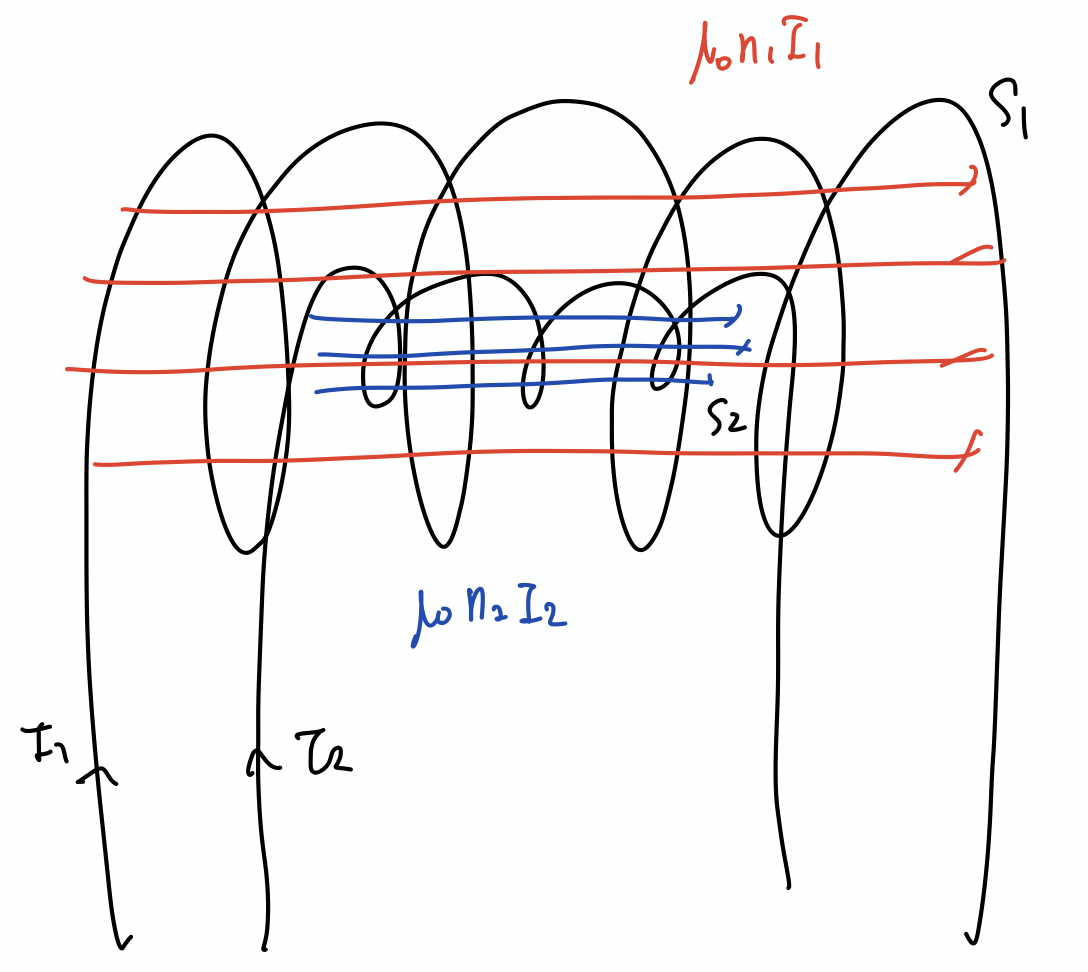
実際に結合係数を計算してみましょう. 上の場合では $$k=\frac{M}{\sqrt{L_1L_2}}=\sqrt{\frac{S_1l_2}{S_2l_1}}$$ となり, これはたしかに $0<k<1$ です（なぜなら図の設定から $S_2>S_1$ かつ $l_1>l_2$ であるので）. 下の場合では $$k=\sqrt{\frac{S_2l_1}{S_1l_2}}$$ となりこれもたしかに $0<k<1$ です. ちなみにこれも合ってそうな結論です。

追記. つまりこのようなコイルは密結合ではないということ。一般的に「密結合でない」は「漏れ磁束がない」と言い換えられるが、この場合は “漏れ” という感じがない……実は「実質的に効いている磁場がどのぐらいか」的な何かが本質なのでは？ たしかに $l_1=l_2$ かつ $S_1=S_2$ とすれば密結合になり、それはたしかに「全磁束が実質的に効果を持っている」ということに対応している。ギャップがあると、無限長近似では相反性がバグらないように磁場を描くことができるものの、結合係数の方にはちゃんと影響が出ているというわけか？

思ったのですが, たぶんよくある「真空中に二つのコイルを置いて相互誘導〜」というのは、たぶん無限長近似を考えると間違っています。というか、実際真空中の透磁率がカスであることを考えると、そう見なすのが適切なはずです。ところが鉄などの強磁性体はオーダーが4桁ぐらい違うので話が全然変わってくるということだと思います。

殴り書きですが一応書いておかないと忘れてしまうので置いておきます。ただやっぱり実験した方がいいね。埒があかないので。解析解は見当たらないというか難しいだろうし、ランダウ・リフシッツにも（媒質中の電磁気学の方は全く読めないけどザーッと目を通したところでは）載ってないし、うーん。

追記. 有限ソレノイドコイルに鉄心を入れると、外では $n$ に依存した磁場ができるが、中では $N$ に依存した磁場ができると考えてよいという噂があるようです。

参考文献

岩田真. (2020). 『電磁気学』. 森北出版.