よく数Ⅱの $3$ 次関数で「接点の個数と接線の本数が一致するから……」という “おまじない” を書くことが多いと思いますが、それと同時に $4$ 次関数などでは一般に成り立たないということもよく注意されていると思います。それは相異なる $2$ つ以上の点で接する複接線が存在してしまうからなのですが、実は複接線が存在するかどうかを判定する方法は非自明であり、普通の入試問題であれば「グラフを描いて何となく目視で『相異なる $2$ 点 $A$, $B$ をいくら曲線上で動かしても $A$, $B$ における接線がともに直線 $AB$ に一致することはない』ことが判断できればOK」ぐらいで済まされるのが暗黙の了解となっています。一般の微分可能な関数について複接線が存在する必要十分条件がどう書けるのかは、結構考えて相談したのですが、正直全く分からないというのが現状です。しかしながら、実用上は次の定理を覚えておけば大丈夫だということは分かりました。
定理.
$f$ が $C^2$ 級で $f''$ の零点集合が孤立点のみからなるとき, 複接線が存在するためには少なくとも $2$ つの変曲点を持つことが必要である.
注意.
$f''$ の零点集合が孤立点のみからなるということは, 視覚的には曲線 $y=f(x)$ が線分である部分を持たないということに等しい.
証明.
曲線 $y=f(x)$ に $x=\alpha,\beta$ ($\alpha<\beta$) で接する直線が存在するとき, その傾きは $$\dfrac{f(\beta)-f(\alpha)}{\beta-\alpha}=f'(\alpha)=f'(\beta)$$ であり, 平均値の定理から $$\dfrac{f(\beta)-f(\alpha)}{\beta-\alpha}=f'(\gamma)$$ を満たす $\gamma\in(\alpha,\beta)$ が存在する. 仮定より区間 $(\alpha,\gamma)$ および $(\gamma,\beta)$ で常に $f''(x)=0$ となることはないのだから, それぞれの区間で少なくとも $1$ 回ずつ $f''(x)$ の符号が変化するので少なくとも $2$ つの変曲点が存在する.
系.
$3$ 次関数のグラフは複接線を持たない.
証明.
$3$ 次関数は変曲点を高々 $1$ つしか持たないので定理の対偶から複接線を持たないことが従う.
問題. (1990年 京大後期理系数学 第1問)
曲線 $y=x^4-6x^2$ に, 点 $(a,b)$ を通る $4$ つの接線が引けるのは, $(a,b)$ がどのような範囲にあるときか, 図示せよ.
実はこの問題は安易に考えると罠にハマってしまいます.
解答.
複接線を求める. 曲線 $y=x^4-6x^2$ に直線 $y=ax+b$ が相異なる $2$ 点 $x=\alpha,\beta$ ($\alpha<\beta$) で接することは $x^4-6x^2-(ax+b)=(x-\alpha)^2(x-\beta)^2$ となることに等しく, これを解くと $a=0$, $b=-9$, $\alpha=-\sqrt{3}$, $\beta=\sqrt{3}$ となる. したがって複接線は $y=-9$ である.
$y=x^4-6x^2$ の $x=t$ における接線は $y=(4t^3-12t)(x-t)+t^4-6t^2$ であるので, 点 $(a,b)$ を通る $4$ つの接線が引けるための必要十分条件は, $t$ の方程式 $$f(t)=3t^4-4at^3-6t^2+12at+b=0$$ が相異なる $4$ 実解を持ち, かつ $b\neq-9$ が成り立っていることである.
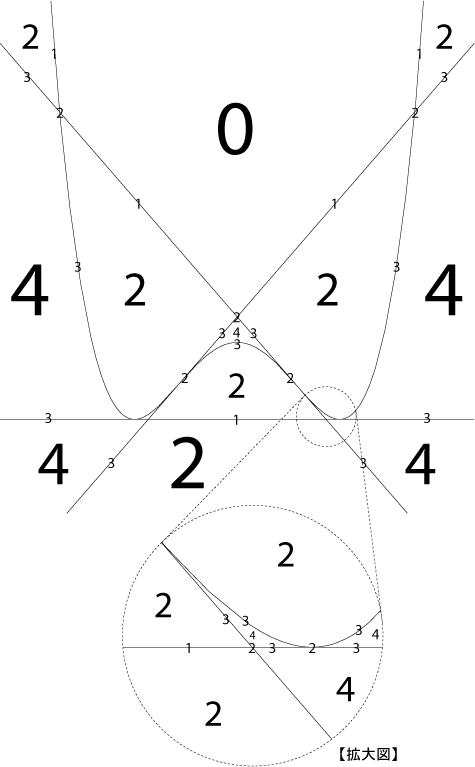
$f'(t)=12(t-a)(t-1)(t+1)$ なので $a\neq\pm1$ が必要であり, 大小に応じて場合分けをする.
斜線部が $(a,b)$ の存在する範囲である. ただし破線と白丸は含まない.
$y=x^4-6x^2$ の $x=t$ における接線は $y=(4t^3-12t)(x-t)+t^4-6t^2$ であるので, 点 $(a,b)$ を通る $4$ つの接線が引けるための必要十分条件は, $t$ の方程式 $$f(t)=3t^4-4at^3-6t^2+12at+b=0$$ が相異なる $4$ 実解を持ち, かつ $b\neq-9$ が成り立っていることである.
$f'(t)=12(t-a)(t-1)(t+1)$ なので $a\neq\pm1$ が必要であり, 大小に応じて場合分けをする.
- $a<-1$ のとき, $f(a)<0$ かつ $f(-1)>0$ かつ $f(1)<0$ であればよい.
- $-1 < a < 1$ のとき, $f(-1)<0$ かつ $f(a)>0$ かつ $f(1)<0$ であればよい.
- $a>1$ のとき, $f(-1)<0$ かつ $f(1)>0$ かつ $f(a)<0$ であればよい.
- $f(a)=-a^4+6a^2+b$
- $f(-1)=-8a-3+b$
- $f(1)=8a-3+b$
斜線部が $(a,b)$ の存在する範囲である. ただし破線と白丸は含まない.
一般の本数については次のような結果が知られています。
実際に計算した記事も存在します. ただし, 最後の節まで二重接線を考慮していないことに注意してください.
