はじめに
電磁気学を教えていたときにボヤいた記事をふと思い出しました.
ここで「合成容量」について色々と書きましたが, 実際に練習問題として解いてもらったものを紹介してみます.
面積 $L ^ 2$ の正方形の極板でできた, 電気容量 $C$ のコンデンサーが真空中に置かれている. このコンデンサーに電圧 $V$ の電池をつないで充電する. 図のように, その後スイッチを開いてから, 極板間に厚さが極板間距離の半分の導体板を極板に平行にゆっくり挿入した. 導体板をコンデンサーのちょうど真ん中まで挿入したとき, コンデンサーから導体板にはたらく力の大きさを求めよ. ただし, 真空の誘電率を $\varepsilon_0$ とする. また, $x\ll1$のとき, $(1+x) ^ n\fallingdotseq 1+nx$ という近似式を用いてよい.
これは三澤 (2019) の 3-4 例題 で, 合成容量の公式を使いながら $\Delta x$ だけ微小変位させた場合に……という流れで求めています. しかし, 別に近似は必要ありません.
準備
次の2点に注意しましょう.
- スイッチを開いた後に挿入しているので, コンデンサーに貯まった電荷は一定となる.
- 導体内電場は $0$ なので等電位となる.
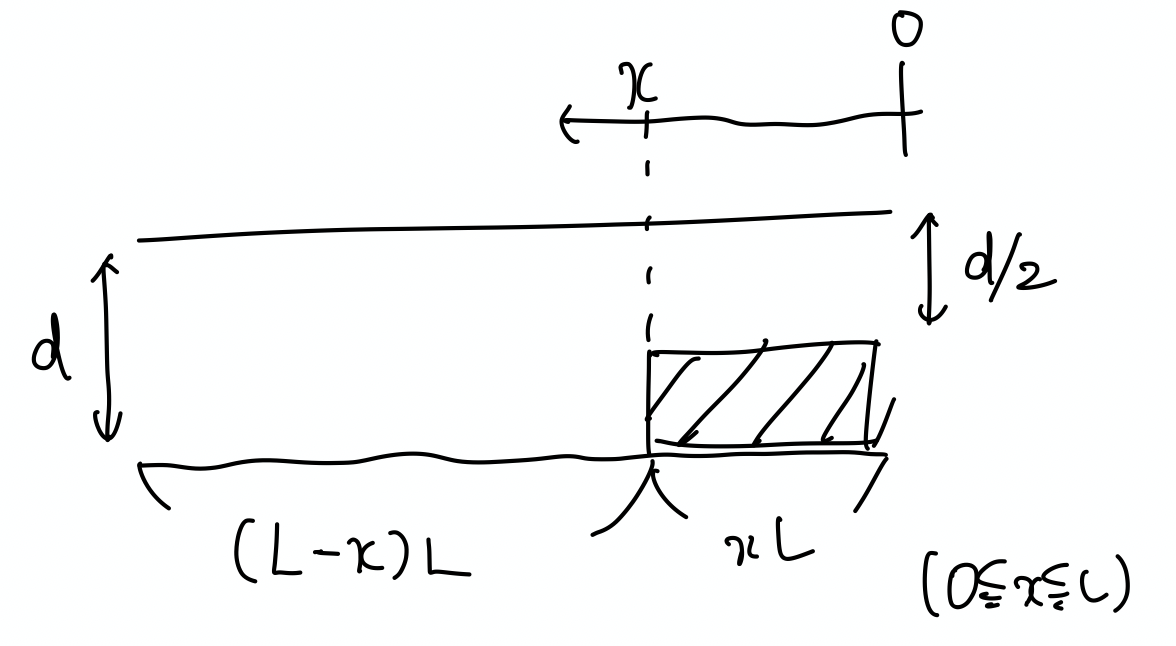
求めるべきは, 導体板に働く静電気力 $F(x)$ の $x=\dfrac{L}{2}$ における値です.
解答
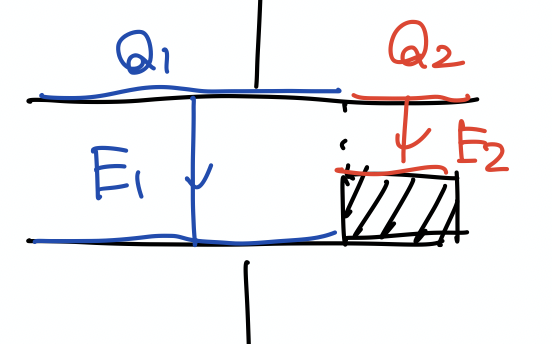
未知数は $Q_1$, $Q_2$, $E_1$, $E_2$, $d$ の $5$ つで, 成り立つ関係式は
$$\begin{cases} E _ 1 = \dfrac{Q _ 1}{\varepsilon _ 0(L-x)L} \\ E _ 2 = \dfrac{Q _ 2}{\varepsilon _ 0 xL} \\ E _ 1\cdot d=E _ 2\cdot\dfrac{d}{2} \\ Q _ 1+Q _ 2=CV \\ C=\varepsilon _ 0\dfrac{L ^ 2}{d} \end{cases}$$
のちょうど $5$ つなので解くことができます. ただし, 1, 2 式目は Gauss の法則, 3 式目は定常状態が等電位で達成されること, 4 式目は孤立系の電荷保存則, 5 式目は一般の平行板コンデンサーに Gauss の法則を適用した結果から従います. 一応すべて計算すると,
$$\begin{cases} Q _ 1 = \dfrac{L-x}{L+x}CV \\ Q _ 2 = \dfrac{2x}{L+x}CV \\ E _ 1 = \dfrac{CV}{\varepsilon _ 0L(L+x)} \\ E _ 2 = \dfrac{2CV}{\varepsilon _ 0L(L+x)} \\ d = \dfrac{\varepsilon _ 0 L ^ 2}{C} \\ \end{cases}$$
となります. したがって静電エネルギー $U(x)$ は,
$$\begin{aligned} U(x) &= \frac{1}{2}Q _ 1 E _ 1 d+\frac{1}{2}Q _ 2 E _ 2 \frac{d}{2} \\ &= \frac{1}{2}(Q _ 1+Q _ 2)\frac{CVd}{\varepsilon _ 0L(L+x)} \\ &= \frac{1}{2}CV ^ 2\frac{L}{L+x} \end{aligned}$$
と計算できます. エネルギー収支は $dU=F_{\text{ex}}dx$ なので,
$$F(x) = -F_{\text{ex}}(x) = -\frac{dU}{dx} = \frac{1}{2}CV ^ 2\frac{L}{(L+x) ^ 2}$$
よって $$F\left(\dfrac{L}{2}\right)=\boxed{\frac{2CV ^ 2}{9L}}$$ です. この値は正であり, たしかにこれは導体板が静電誘導によってコンデンサーの表面の電荷と逆符号に帯電していることで引き込む向きの静電気力を受けているという定性的な議論と一致していることを表しています.
参考文献
三澤信也. (2019). 『分野をまたいでつながる高校物理』. オーム社.