はじめに
2017 年度の大阪大学*1と京都大学*2の物理の入試問題において,音波に関する取り扱いが不適切であったことが判明し,それぞれに追加合格者が出たことはまだ記憶に新しいです.いずれも音波を変位波と扱うか密度波と扱うかを混同していることが原因であり,充分に注意しなければ容易に誤った結論を導いてしまいます.このことは,音声学の名著である『ビジュアル音声学』の図 3.2.3-2 において致命的なミスが起こっていることからも窺えます.結論としては「(変位波をやめて)密度波にかえれ」ということになります.
出題ミス
大阪大学と京都大学の出題ミスが本質的にはどのようなものだったのかというと,誤解を恐れずに言えば
| 音叉から出る音波 | 固定壁 | |
|---|---|---|
| 変位波 | 逆位相 | 固定端反射 |
| 密度波 | 同位相 | 自由端反射 |
という混乱を招きやすい関係に原因があります.この点についての物理学的な解説のうち最も信頼できる文書は冨田博之「高等学校物理「音波」における混乱の要因」なので,詳しくはぜひそちらを読んでみてください.
ビジュアル音声学
音声学は音声を扱う学問ですが,音声はヒトが発するものであり,それは耳のうずまき管によって受容されます.うずまき管に振動が伝えられるのは,音波が外耳道を通って鼓膜を振動させ(て耳小骨で増幅されて卵円窓を強制的に振動させ)るからですが,実は鼓膜の後ろが閉鎖されている構造を持つことによって,鼓膜は変位ではなく圧力変化(つまり密度変化)を検出していることになります.したがって,音声学的に適切な音波の描像は,変位波としてではなく密度波としてであると考えられると個人的には思います.
ただ,それはそれとして,次の記述をご覧ください.
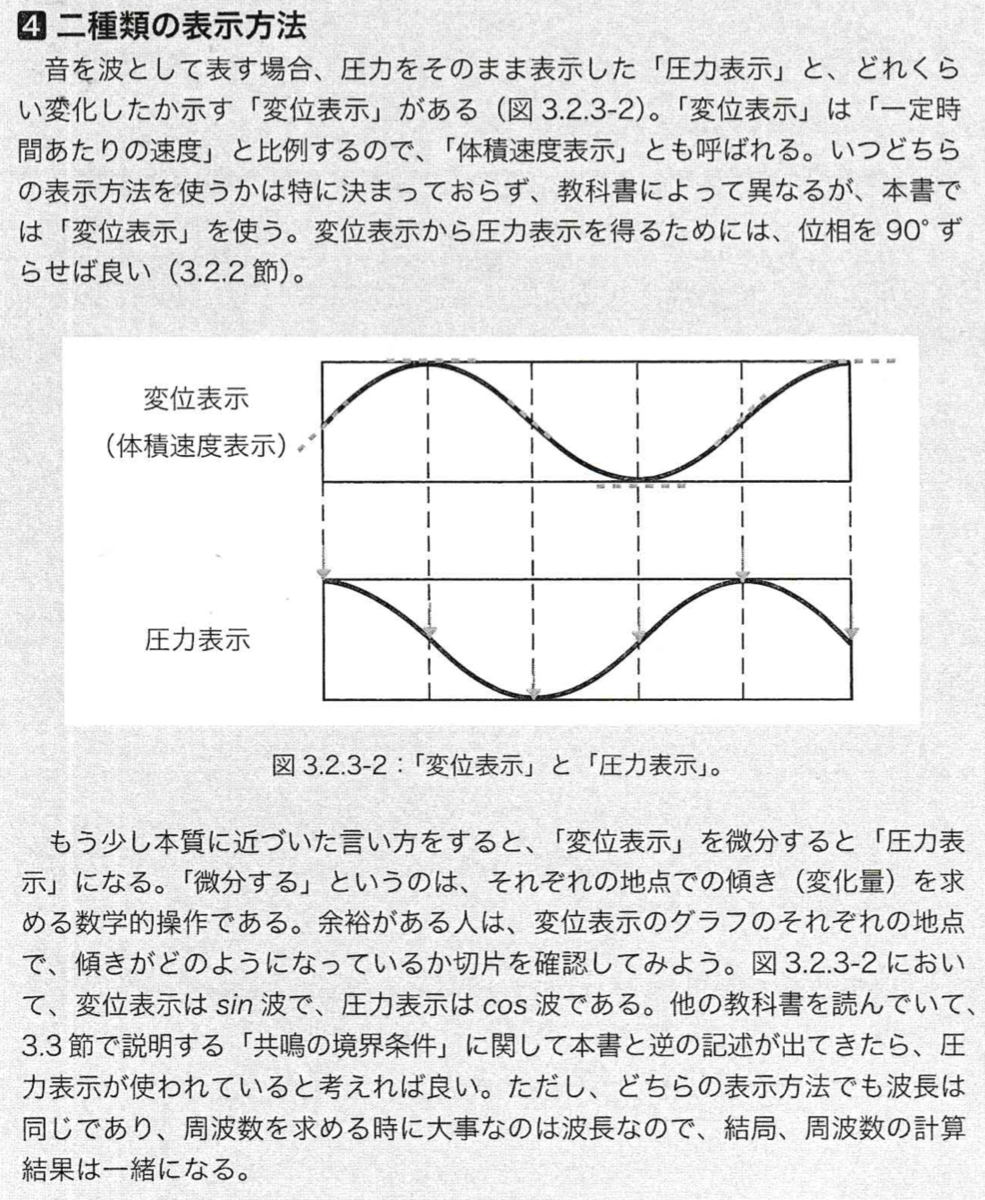
常識的に解釈すれば,変位表示の縦軸は中心が変位なしで上側が正の変位であり,圧力表示の縦軸は中心が大気圧で上側が高い圧力でしょう.本書では変位表示がメインなので,ここでは変位表示のグラフから圧力表示のグラフを得ることを考えましょう.
ある地点での圧力を考えたいとします.このとき,その地点を含む微小な区間を考えて,負の側にある端の変位と正の側にある端の変位を読み取ります.
- もし負の側が正の方向に変位していて,正の側が負の方向に変位していれば,それは「両側から押されている」というイメージになるので,圧力は当然大きくなり,密度は密になります.
- もし負の側が負の方向に変位していて,正の側が正の方向に変位していれば,それは「両側が離れていく」というイメージになるので,圧力は当然小さくなり,密度は疎になります.
- もし負の側も正の側も同じ方向に同じだけ変位していれば,それは「平行移動しているだけ」というイメージになるので,圧力は変化せず,密度も変化しません.
このように定性的に読み取ることができるので,変位が正弦波的に変化していくのであれば,圧力も正弦波的に変化していくだろうと充分合理的に考えられることを加味して,次のような対応を得るはずです.

図 3.2.3-2 では上下真逆になっているので完全に誤りです.このことは,図 3.2.3-3 (a) の二段目と四段目をよく眺めると視覚的に納得できるでしょう.

もちろん,高校物理を多少でも勉強したことがあれば,$$\frac{\Delta\rho}{\rho_0}=-\frac{\partial y}{\partial x}(x,t)$$のような定量的評価を導き出すモデルや,音波の伝播が理想気体の準静的断熱変化と見做せるので Poisson の法則を使って圧力変化 $\Delta p$ が密度変化 $\Delta\rho$ に比例することを知ることになりますが,それと同時にこういった定性的な見方ができるという事実も大事です.ちなみに,p. 107 には
もう少し本質に近づいた言い方をすると、「変位表示」を微分すると「圧力表示」になる。
という記述がありますが,定性的な議論からも上の表式からもわかるように,「微分すると」ではなく「微分して符号を逆にすると」です.
密度波にかえれ
先ほど「変位波はヒトの生理学的機構と合わないので密度波を考えたほうがよい」と主張しましたが,実はより強く「変位波は物理学的実体に基づいておらず密度波が正しい描像である」とまで言えます.
高校物理で使われている縦波の「変位」は,平衡位置のない空気のような流体では,考えてみると奇妙な概念なのであるが,流体が静止していたときの位置からの変位,いわゆる流体粒子の座標変位として無反省に使うことにする。
やっかいなことに、大学以降では、音波は偏微分方程式と境界条件で記述するので、言葉が完全に変わる。壁での境界条件は、密度や圧力は自由境界、変位や速度は固定境界である。特に、密度波で記述することが圧倒的に多くなり、変位波を使うことはほぼない。そこでは、「音波が固定端反射する」という言葉すら、もはや完全に意味不明になる。
佐々真一「高校物理における音波の解説」(現在は非公開)
そのことを如実に示す例を見てみましょう.
図 1 のように置いた二つの音源 S1,S2 から振動数,振幅,位相が同じ正弦波の音波が発せられている。音源の前方にある直線 AB 上での音の聞こえ方を調べたところ,S1,S2 から等距離の点 O では音が最も大きく聞こえた。点 O から直線 AB 上にそって離れるとしだいに音の大きさが小さくなり,点 P ではじめて極小となった。さらに点 O から離れていくと今度はしだいに音が大きくなり,点 Q で音の大きさは再び極大となった。
2004年 センター 物理 IB 第 4 問 A 図 1
先ほど述べたように,ヒトの生理学的機構により音の大小は変位の正負ではなく密度(あるいは圧力)の大小に対応するのでしたから,この点 O では圧力が最大になっており,そこから左右に極小,極大,極小,極大,……を繰り返すということになります.この大小の分布は(疎密のイメージを考えると何となく納得できると思いますが)音源と直線 AB の距離によらず同じです.特に,二つの音源から等距離の点の集合(この直線を L とおきましょう)は音の大きさが極大となる「稜線」になります.
しかし,変位波で考えるとどうなるでしょうか.まず簡単ですが重要なこととして,音源 S1 と S2 を結ぶ線分において音の大小がどうなるのか考えてみましょう.一番最初に述べたように,音源から出る音波は変位波としては逆位相で出るのでした.振動数,振幅,位相が同じ正弦波が互いに逆向きに進行して重なり合うと,定常波ができるのでした.したがって中点では節になり,そこから左右に腹,節,腹,節,……を波長の四分の一ごとに音源の位置に来るまで繰り返すことになります.前の定性的な考察から,この場合は節の位置で密度変化が最大になります.もちろん,この議論は横波と近似できるような水面波には通用しません(お風呂で実験してみてください).
ところが,音源の中点から直線 L 上に沿って離れていくと,S1 と S2 から出る音波の変位のなす角(変位はベクトル量でした!)はどんどん小さくなっていき,したがってどんどん互いに強め合うようになっていきます.直線 L は中点では節であり,そこから少しずつ変化していって,無限遠方では腹線になってしまいます.しかしながら,密度波の観点では,当然ながらこの直線 L はずっと音の大きさが極大の点が連なっていることになります.したがって,一次元であれば「節が密度変化最大であり,腹が密度変化最小である」と言えますが,二次元であれば必ずしもそうとは言えなくなってしまいます.

この議論自体は元々とある方から教えていただいたものでしたが,最近なんと 2004 年に石川昌司「音波の指導で気になっていること」という論文で書かれていることを知りました.最後に,第 4 節の「変位波の問題点」を引用して,本稿を終えることにしましょう.
そもそも,音波の「変位」とは一体何を指しているのだろうか.実際の「空気」は「分子」が集まってできているのであり,空気「分子」はそれぞれが熱運動している.変位とは,それらの分子の単位量毎に気体をメッシュに分割して,そのブロックの内の分子の平均位置を基準位置に比較して定義しているのだろうか.しかし,この定義は高校生にとってはかなり難解であろう.
また,仮に,このような定義を受け入れたとしても,例えば1で扱った問題のような,気柱の閉口端で「変位」が固定されている事実は単純には導けない.なぜなら,メッシュに分割されたブロック内で分子は自由に運動しているからである.つまり「閉口端はその付近の空気分子の位置平均は動かないので固定端になる」という説明は少なくとも自明ではない.
仮に分子の存在を無視して,空気を連続弾性体とみなして近似するにしても,問題は簡単には解決しない.閉口端近くの空気が変位してしまえばその部分が真空になってしまうから,それは矛盾なのでやはり変位は $0$ でなければならないというような説明は一見説得力があるようにも思えるが,実際には,閉口端は最も密度変化の激しい点のひとつであって,閉口端の空気は周期的に真空に向かって変化していることを考えると,このような説明にはそれほど強い賛同は得られない.結局,物理量は連続的であるべきだという,連続性または接続性の要請を持ち出さない限り,うまく説明できないように私には思える.
つまり,空気の変位に基づく音波の説明は,最初はわかり易そうに見えるのだが,しかし,少し深く考えて見てみるとなかなかやっかいな問題が後に控えているということがわかる.
