概要
本記事は, すでに中止となった令和二年度の数研合宿のために用意していたOB講義案をまとめたものです. 対象部員は中学三年生あたりを想定しております. Doppler 効果は基礎的で簡単な現象ではありますが, むしろそれゆえに多くの物理的示唆に富んでいる代表的な話題であると言えます. 例年のOB講義は受験や競技などを超越した話題を展開することに主眼がありますが, 今回はあえて受験を中心に据えつつ, 同時に物理学への入門としても有益な内容になることを目指しました.
舞台設定
物理学は非常に西洋的な思想に端を発していますが, その適用範囲はあまりに多岐に渡っており, 現代の自然科学や科学技術を理解する上で極めて重要な学問になっております.
21世紀の現在まで物理学は異常なスピードで発展し続けて来ましたが, その中でも17世期に始まり19世期半ばに一段落ついた古典物理学を中学高校では主に学習することになります. その世界像は「$3$ 次元の一様・等方な空間の中で, 一様な時の流れでの極めて多数の “素粒子” の運動が自然現象である」というものです.
空間と時間については古典物理学のなかでも色々議論する必要がありますが, 今回の振動・波動論ではひとまず空間を $3$ 次元 Euclid 空間, 時間を $1$ 次元 Euclid 空間として議論を始めることにしましょう.
また, 時代が降るにつれて “素粒子” の指すものが現代物理学的により精確になるので, 古典物理学では「粒子」と呼び分けて次のように定義されていると考えていただいて構いません.
物理学では粒子の運動がある種の体系に従っているはずだと考え, それは粒子間の基本相互作用 (いわゆる力) に基づいていると考えることで現代にいたるまで様々な成果をあげることに成功しました. 現代の物理学では基本相互作用を次の四種類に分類しています.
- 重力
- 電磁気力
- 強い相互作用
- 弱い相互作用
強い相互作用と弱い相互作用は非常に微小な有限区間にしか届かないので古典物理学で考察する必要が一切なく, 対照的に重力や電磁気力は無限に遠くまで届くので古典物理学でもこの二つの力を考える必要が出てきます.
地球の表面付近に現れる力の古典物理学的な扱いは次のようにすればほぼ問題ありません.
- 物体と地球の重力のみを考えれば十分で, 他の物体との重力は弱すぎるので無視します.
- 電気的に中性のマクロな物体同士には基本的に電磁気力は働かず, 物体が接触しているときにのみ接触面の構成分子間の電磁気力のみを考えます.
一般にミクロな電荷分布を知ることは不可能ですから電磁気力が存在すること自体はわかっていても古典物理学的にどう現れるかはわかりません. 今回はあえて扱いませんが, 古典力学ではそういった力は運動方程式や束縛条件で決めるものなのです. ところが, 例外的にその応力がマクロな変位の関数で表される場合があり, その物体を弾性体, その力を弾性力とよびます*1.
弾性体は分子の結合という離散的な構造をもっているわけですが, それを捨象して, 空間的な広がりをもつ変形可能な連続体と考えてみると, 連続体の一点に励起された振動は応力を介して連続体の広域的な振動を連鎖的に誘起します. これを波動(波)とよび, その連続体を(波の)媒質, その一点を波源とよびます.
波動は次の二種類に分類されます.
- 力学的波動: 力学的媒質の振動が媒質間の応力により伝わる現象
- 電磁波 (光): 電磁場の振動が Maxwell 方程式に従い伝わる現象
ここで古典電磁気学に立ち入ることはしませんから, 電磁波についてはひとまず天下りに考えてください. とにもかくにも, 次の事実が最も本質的で重要なことなのです.
Doppler 効果の本質はこの事実にあります.
波動の表現
本来であれば力学的波動は連続体力学, 電磁波は古典電磁気学を理解しそのメカニズムを解明した上で考えるべきでしょうが, Doppler 効果を理解する上では不要です. 何が必要かといえば, それは波源から空間的に離れた観測者が観測する振動を一般に表現することです. すなわち波源を原点とした観測者の位置ベクトル $\bm{r}$ と時間 $t$ の関数 $\psi(\bm{r},t)$ として振動の変位を表現することです.
しかし無闇矢鱈に複雑な考察をしても Doppler 効果という現象の理解には役に立ちませんから, まずは $1$ 次元波動を考えます. また, 波の伝播速度は媒質の状態に依存しますが, 媒質の状態が一様一定の場合のみを考えることで, 波の伝播速度が一様一定で $c$ であると考えます.
また, 現実世界の一般の波はすべて正弦波の重ね合わせで表現できる(Fourier 変換)ことが知られているので, 正弦波を考察することが非常に重要になります. 正弦波とは, 波源の振動の変位が, 正の定数 $a$ を用いて $\psi(0,t)=a\sin\theta(0,t)$ と表されるような波のことです. 最大変位 $a$ を振幅といい, $\theta(0,t)$ を位相 (phase) といいます. ただし, $\theta(x,t)$ は $x$ と $t$ の $1$ 次関数だとします.
ここで, $\sin\theta\equiv\sin(\theta+2\pi)$ なので, 位相が $2\pi$ ずれることを $1$ 回の振動と数え, 単位時間あたりの振動回数を振動数 (周波数) といい, $f$ で表します. したがって, 初期位相 $\theta(0,0)$ を $\alpha$ とおくと, $\theta(0,t)=2\pi ft+\alpha$ となります.
時刻 $t'$ の波源の振動が時刻 $t$ に観測者に届いたとすると, 観測者が時刻 $t$ に観測する振動の変位は, 途中に反射などにより生じる位相のずれ $\beta$ を考慮して $$ \left\lbrace\begin{aligned} \psi(x, t) &=A \sin \left(2 \pi f t^{\prime}+\alpha+\beta\right) \\ t &=t^{\prime}+\frac{x-0}{c} \end{aligned}\right. $$ となるので$$\psi(x,t) = A\sin\left(2\pi f\left(t-\frac{x}{c}\right)+\alpha+\beta\right)$$となります. ここで $A$ は観測者の観測する振動の振幅で, エネルギーの散逸などが生じるため一般には $A\leq a$ となりますが, ひとまず振幅の減衰を無視して $A=a$ と考えます.
$x$ を固定すると $\psi(t)=a\sin(2\pi ft+\cdots)$ となり, ビヨンビヨンと周期的に行ったり来たりする現象が見られます. これを単振動といいます. 振動数は $f$ ですが, $1$ 回振動するのにかかる時間, すなわち $t$ としての周期を周期といい, $T=\dfrac{1}{f}$ の関係が成り立っています.
$t$ を固定すると $\psi(x)=a\sin\left(2\pi f\cdot\dfrac{x}{c}+\cdots\right)$ となり, $\psi=a$ となる山と $\psi=-a$ となる谷が交互に周期的に並ぶことがわかります.
谷と谷の間隔, すなわち $1$ 回振動する時間 $T$ の間に波の伝わる距離, すなわち $x$ としての周期 $\lambda$ を波長といいます. $\psi(x+\lambda,t)=\psi(x,t)$ をみたす最小の $\lambda$ ($>0$) なので $2\pi f\cdot\dfrac{\lambda}{c}=2\pi$ すなわち $\lambda=\dfrac{c}{f}=cT$ です. また, $1$ 秒間に $c$ だけ進むということは $T$ 秒間で $cT$ 進むということなのでたしかに $\lambda=cT$ です.
$1$ 回の振動でできる波を $1$ 個と数えるので, 長さ $2\pi$ あたりの波の個数を波数 $k=\dfrac{2\pi}{\lambda}$ といいます. 時間 $t$ の間にある波の個数は $ft$ となります.
Doppler 効果
波源から観測者へ波が伝わる時間は有限であり,
- 波源と観測者の相対的距離
- 波の伝わる速度
に依存するので
- 波源と観測者の相対的距離が時間的に変化すること
- 媒質の状態が時間的に変化することなどにより, 波の伝わる速度が時間的に変化すること
で波源から観測者へ波の伝わる時間が, その出た時刻により変化するとき, 波源の周期や振動数と異なる周期や振動数の波が観測される現象が起こり, これを Doppler 効果といいます.
波源が近づいてくるときは, ある瞬間に出た波が観測者に届くまでの時間より, その少し後に出た波が観測者に届くまでの時間の方が(波源と観測者の距離が短くなっている分だけ)短くなってしまいます. このとき観測される周期は波源の周期より短くなり, 振動数は高くなります. 遠ざかる場合は逆です. ただし, 観測者にとって波の伝播速度が無限大とみなせるときは全部同じです. (cf. 事実1.2)
救急車が近づくときは高い音, 遠ざかるときは低い音になるということが定性的にわかります.
簡単な例として次のような場合を考えてみましょう. ただし $\dfrac{|u|}{c}, \dfrac{|v|}{c}\ll 1$ とします.
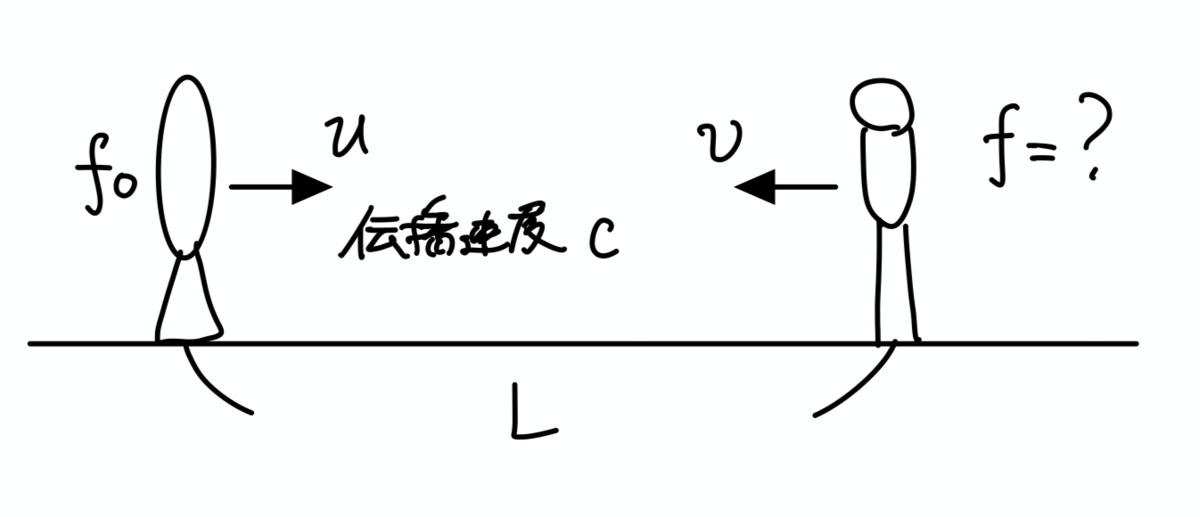
導出1
波の表現を用いてみましょう. 時刻 $t'$ に出た波が時刻 $t$ に届くとすると
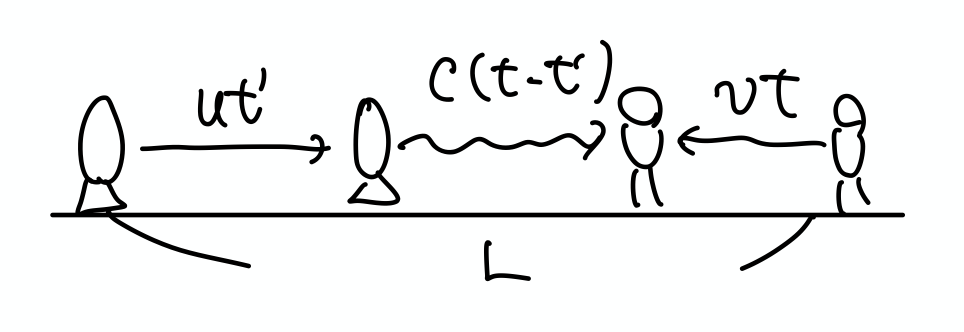
$$\left\lbrace\begin{aligned} L &= ut'+c(t-t')+vt\\ \theta_{\text{O}}(t) &= 2\pi f_0 t' \end{aligned}\right.$$
これを解いて $\theta_{\text{O}}(t)=2\pi f_0 \dfrac{c+v}{c-u}t+\cdots$ となるので $f=\dfrac{c+v}{c-u}f_0$ です.
導出2
出たタイミングによる所要時間のズレを求める最も直接的な導出です.
波源が $t=0$ から $t=\Delta t$ までに出した波の数と, 観測者が $t=T$ から $t=T+\Delta T$ までに受け取った波の数は同じなので, $f_0\Delta t=f\Delta T$ が成り立ちます.
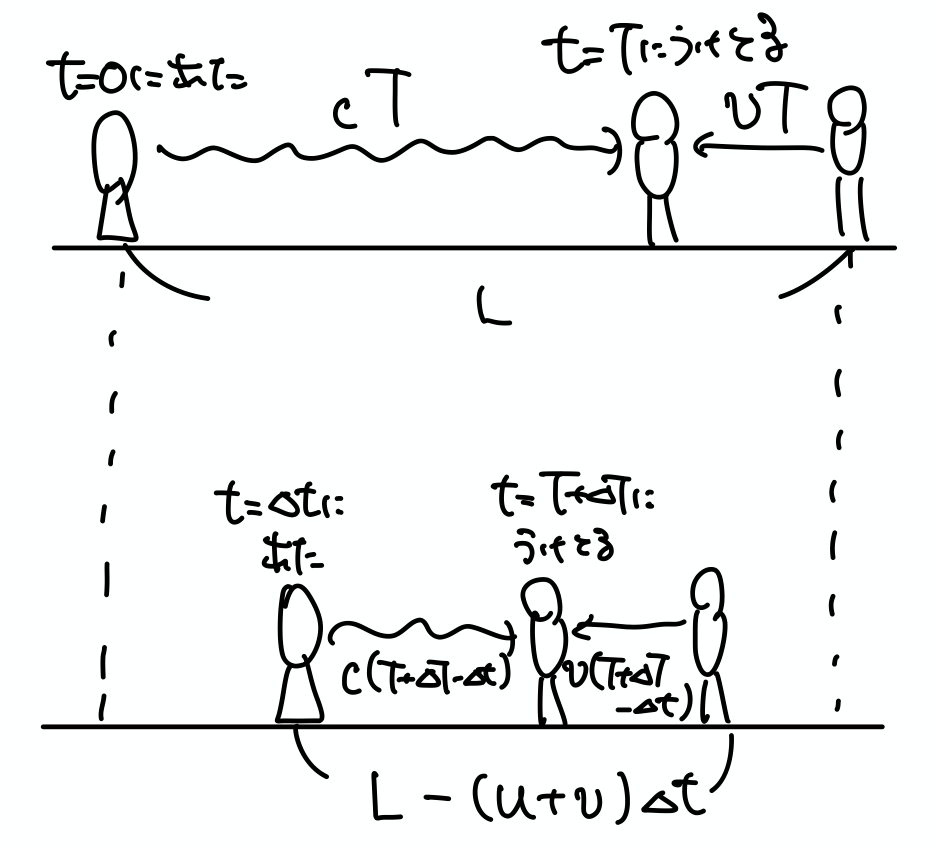
$$\left\lbrace\begin{aligned} L &= (c+v)T\\ L-(u+v)\Delta t &= (c+v)(T+\Delta T-\Delta t) \end{aligned}\right.$$
より $\Delta T=\dfrac{c-u}{c+v}\Delta t$ なので $f=\dfrac{c+v}{c-u}f_0$ となります.
導出3
観測者からみた波の速度は $c'=c+v$ です. あるいは観測者は単位時間あたり $c'$ の距離の中の波と出会います.
観測者からみた波長は「単位時間に出た $f_0$ 個の波が距離 $c-u$ の中に含まれる」ので, $\lambda'=\dfrac{c-u}{f_0}$ です.
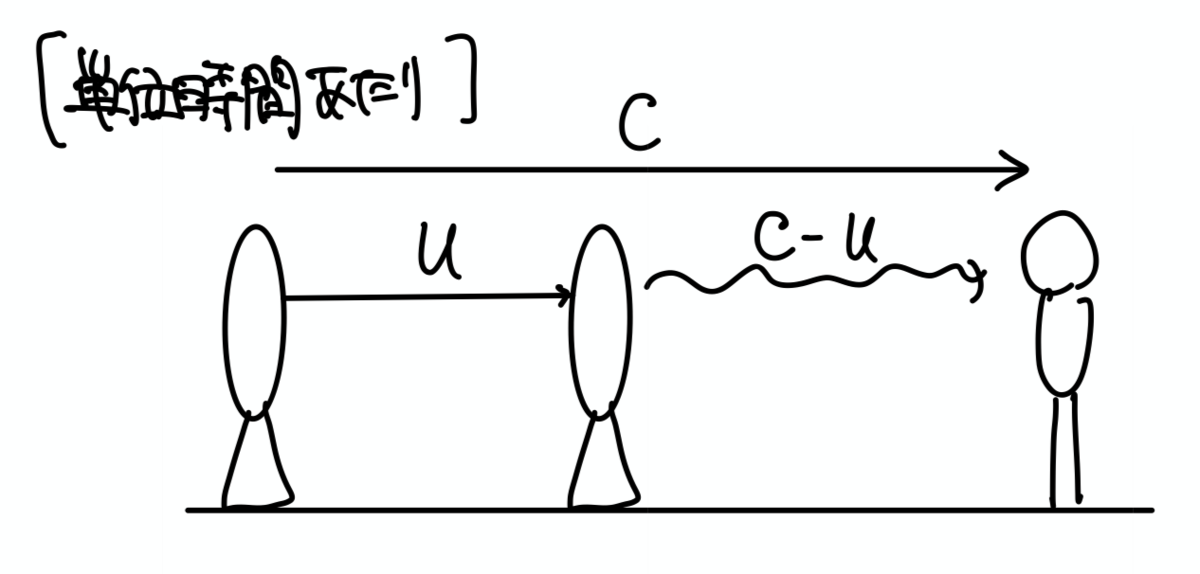
したがって, 観測者は単位時間あたりに距離 $c'$ の中に含まれる波と出会い, 波1個あたりの間隔が $\lambda'$ であるから, $f=\dfrac{c'}{\lambda'}=\dfrac{c+v}{c-u}f_0$ です.
斜めDoppler効果
振動数 $f_0$ で振動することにより音を発生する装置をもつ音源が, 周囲に音を出しながら, 音速 $c$ より遅い速度 $v$ で, 等速直線運動をしている. 定位置Aで音の振動数を測定する. 音源の運動する直線上に点Bをとる. A, B間の距離は $L$ であり, Bから見てAは音源の速度方向と角度 $\theta$ の方向にある(図1).
音源がBに到達する瞬間に出す音波と, それから音源の振動の一周期後に出す音波とは, 測定点Aに時間差 $T=\fbox{ イ }$ で到着する. 音源の振動数 $f_0$ が $v/L$ に比べ充分大きいときは, 音源がBを通過しながら出す音が, Aでは振動数 $f$ の音として聞こえる. この場合, 時間差 $T$ を与える式から, 振動数 $f$ は $f_0$, $c$, $v$, $\theta$ を用いて $f=\fbox{ ロ }$ とあらわすことができる.
必要ならば次の近似式を用いよ. $|x|$ が $1$ に比べ充分小さいときは $(1+x+bx^2)^{\alpha}\fallingdotseq 1+\alpha x$.

これは導出2です. 音源の振動の一周期 $\dfrac{1}{f_0}$ の間に音源がBから進んだ位置をCとおき, $L'=\text{AC}$ とおくと, $$L'^2=L ^ 2+\left(\dfrac{v}{f_0}\right) ^ 2-2L\dfrac{v}{f_0}\cos{\theta}$$です. BおよびCからの音波がAに到達する時間差 $T$ は $$\begin{aligned} T &= \dfrac{1}{f _ 0}-\dfrac{1}{c}(L-L') \ &= \frac{1}{f _ {0}}-\frac{L}{c}\left\lbrack 1-\left\lbrace 1-2 \frac{v}{L f _ {0}} \cos \theta+\left(\frac{v}{L f _ {0}}\right) ^ {2}\right\rbrace ^ {1/2}\right\rbrack\ &\fallingdotseq\left(1-\dfrac{v}{c}\cos{\theta}\right)\dfrac{1}{f_0}\end{aligned}$$ なので $f=\dfrac{c}{c-v\cos{\theta}}f_0$ となり, 視線速度 $v\cos{\theta}$ で近づいてくるときの公式と一致しています.
Lorentz 因子
さて, 天体Xからこの過程をみるとどうなるだろうか. 宇宙人にとっては, 逆に地球が速度 $v$ で天体Xに近づいてくるように見える. 天体Xでこの光の速度が $c'$ であったとすると, 地球での振動数 $f_2$ は $\fbox{ B }$ となる.
この2つは同じ現象を違う立場からみたものなので, 結果は等しいはずであり, そのためには $c'$ と $c$ は異なる値でなければならない. ところが, 天体Xでも光速は地球と同じ値 $c$ であることが判明した. この矛盾を説明できる可能性として次のような仮説をたてる.
「地球人からみると, 地球上で単位時間だけ経過する間に, 地球に対して速度 $v$ で運動している天体X上では時間 $k$ が経過する」
すると, 地球の単位時間に天体Xから発射される光の波形がもつ山の数は $f$ ではなくその $k$ 倍になるので, $f_1$ も $k$ 倍しなければならない.
もし, 物理法則が地球と天体Xとで異ならないならば, 同様に次の仮説が成立するはずである.
「宇宙人からみると, 天体Xで単位時間だけ経過する間に, 天体Xに対して速度 $v$ で運動している地球上では $k$ 秒が経過する」
この仮説を用いると, $f_2$ は $\fbox{ C }$ 倍されなければならない. このとき, $f_1$ と $f_2$ が等しいためには, $k=\fbox{ D }$ であればよい. これは, アインシュタインの特殊相対性理論から導かれる結論そのものである.
公式より $\fbox{A}$ $f_1=\dfrac{c}{c-v}f$, $\fbox{B}$ $f_2=\dfrac{c'+v}{c'}f$ となり, $f_1=f_2\iff c'=c-v$ で $v\neq 0$ より $c'\neq c$ です. ところが実験によると常に $c'=c$ が成り立っています. しかしながら同じ現象を違う立場から見ても結果は等しいはずなので, 今までに立てたモデルが不適切であった可能性があります.
そこで所要時間をイジってみることにします. 「地球人から観測すると, 地球での $1$ 秒は天体Xでの $k$ 秒」, それと対称的に「宇宙人から観測すると, 天体Xでの $1$ 秒は地球での $k$ 秒」という仮説を置いてみましょう. 波の数は立場によらないので, それぞれ $k$ 倍, $\fbox{C}$ $\dfrac{1}{k}$ 倍されることに注意すると $kf_1=\dfrac{f_2}{k}$ より $\fbox{D}$ $k=\sqrt{1-\dfrac{v ^ 2}{c ^ 2}}$ となり, これは Lorentz 因子の逆数です.
簡単な帰結として, $k\in\mathbb{R}\iff |v|\leqq c$ です. 科学啓蒙書でもお馴染みの「すべての物体は真空中の光速を超えた速さで動くことはできない」という結論が出てきましたね.
さいごに
Doppler 効果は事実1.2「波動の伝播速度は有限である」に起因する現象であるということを実感していただけたでしょうか. 最後に応用例とその展望について説明して締めることにいたします.
まず, 時間の都合で扱いませんでしたが, 複数の波が重ね合うときに干渉という現象が起こることがあり, その代表現象の一つとしてうなりがあります. Doppler 効果とうなりを組み合わせることで, 自動車の速度違反取締りや野球の球速測定に用いられるスピードガンや, 血流測定に用いるような医療用超音波検査装置の原理が説明されます.
また, 光の Doppler 効果は惑星の観測にも使われます. 惑星からの光はあまりに弱くて直接観測するのは不可能なのですが, Doppler 効果を利用すれば間接的に観測することが可能になります. 2006年 東京大学 第1問 Ⅱ がこのことを出題しています.
そして古典物理学を超えた現代物理学の世界でも Doppler 効果はまだまだ利用価値のある現象です. その代表例がレーザー冷却です. 気体分子の温度を絶対零度近くまで冷却するのは当然大変ですが, そこで Doppler 冷却という手法が存在しており, これは入試問題でもネタとして使われることがあります. 原子分野について説明するのは絶対に時間が足りませんから皆さんの自習課題として割愛させていただきます. また, 原子炉の安定性にも Doppler 効果は関わっています. これは入試問題としては見たこともなく出されもしないだろうとは思いますが, 我々の社会の基盤となっている科学技術を理解するという点では非常に重要なことでしょう.
なお, 今回の振動・波動論ではひとまず空間を $3$ 次元 Euclid 空間, 時間を $1$ 次元 Euclid 空間として議論を始めることにしましたが, 問題3.3からも示唆されるように相対論ではこの仮定にメスをいれることになります. そして非相対論的な現象はあくまでも物体の速度が光速に比べ十分小さいときの近似にすぎなかったと解釈するわけです. 実は Doppler 効果, とくに光の Doppler 効果は, 相対論的にもう一度議論し直す必要があります*2. こうして物理学はモデルを作っては検証し破棄し作っては検証し破棄し……という絶え間なきプロセスのもとに成り立っているのです. それが数学と自然科学の相違点の大きな一つなのです.