$$f(x) = \frac{(1+x ^ 2)^{1/3}}{(1+\cos x)^{3/2}} \frac{\log x}{x ^ 2}$$ のような複雑な関数を微分することになったとき, いちいち商の微分法と連鎖律を使っていては非常に大変ですから, Feynman は「微分可能な関数 $f\colon\R\to\R$ が $f'(x)=f(x)(\log{f(x)})'$ を満たす」ことを利用して次のような微分法を考えました.
- $f(x)$ の横にカッコを書く.
- 各項を $$\text{指数}\times\frac{\text{その項の微分}}{\text{その項}}$$ と変換してカッコの中に書く.
- 整理する.
というわけでまずは
$$f'(x) = \frac{(1+x ^ 2)^{1/3}}{(1+\cos x)^{3/2}} \frac{\log x}{x ^ 2} \bigg( \cdots \bigg)$$
と書き, 分母にある項は指数が負になることに注意するとカッコ内は
$$\left( \frac{1}{3} \frac{2x}{1+x ^ 2} - \frac{3}{2} \frac{-\sin x}{1+\cos x} + 1\cdot\frac{1/x}{\log x} - 2\cdot\frac{1}{x} \right)$$
となります. あとはテキトーに整理してあげてください.
このテクニックは商の微分法のエレガントでより一般的な代用品にもなっています. 実際, Feynman は $g(x)=\dfrac{x ^ 2}{1+x ^ 2}$ のような関数もこのやり方で微分していたそうです*1.
$$\begin{aligned} g'(x) &=\frac{x ^ 2}{1+x ^ 2}\left(2\cdot\frac{1}{x}-1\cdot\frac{2x}{1+x ^ 2}\right)\\ &=\frac{2x ^ 2(1+x ^ 2)-2x ^ 4}{(1+x ^ 2) ^ 2x}\\ &=\boxed{\frac{2x}{(1+x ^ 2) ^ 2}} \end{aligned}$$
先ほど注意したような場合の例も計算しておきましょう.
$$h(x)=\frac{x ^ x}{2^{\sin ^ 2x}}$$
- $x ^ x$ からは $1\cdot\log{x}$ と $x\cdot 1/x$,
- $2^{-\sin^{2}x}$ からは $(-\sin^{2}x)'\log{2}=-2\log{2}\cdot\sin{x}\cos{x}=-\log{2}\cdot\sin{2x}$
が出ることに注意すると,
$$h'(x)=\frac{x ^ x}{2^{\sin ^ 2x}}(\log{x}+1-\log{2}\cdot\sin{2x})$$
Wolfram Alpha 先生に投げてみましょう.
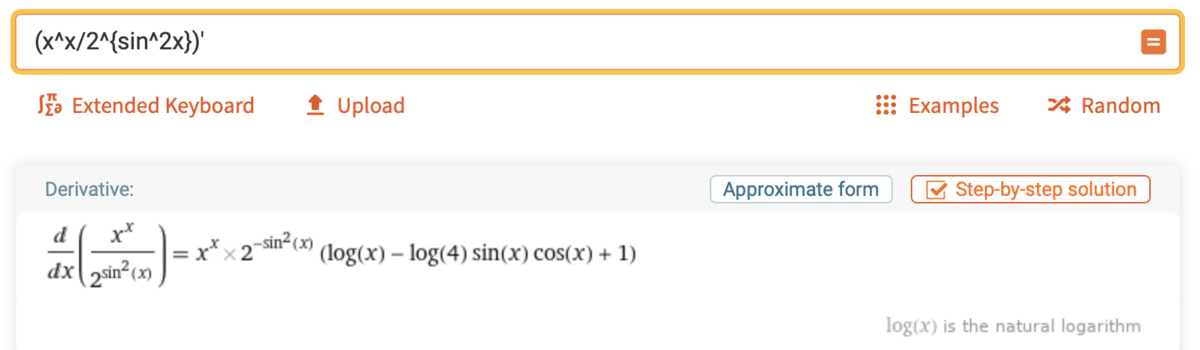
優勝!😉
参考文献
Neer, J. T. (1970-1971). Feynman Hughes Lectures, 5, 10-11.
*1:ただし講義録にある計算は分母を $1+x$ と見間違えているので誤っています.