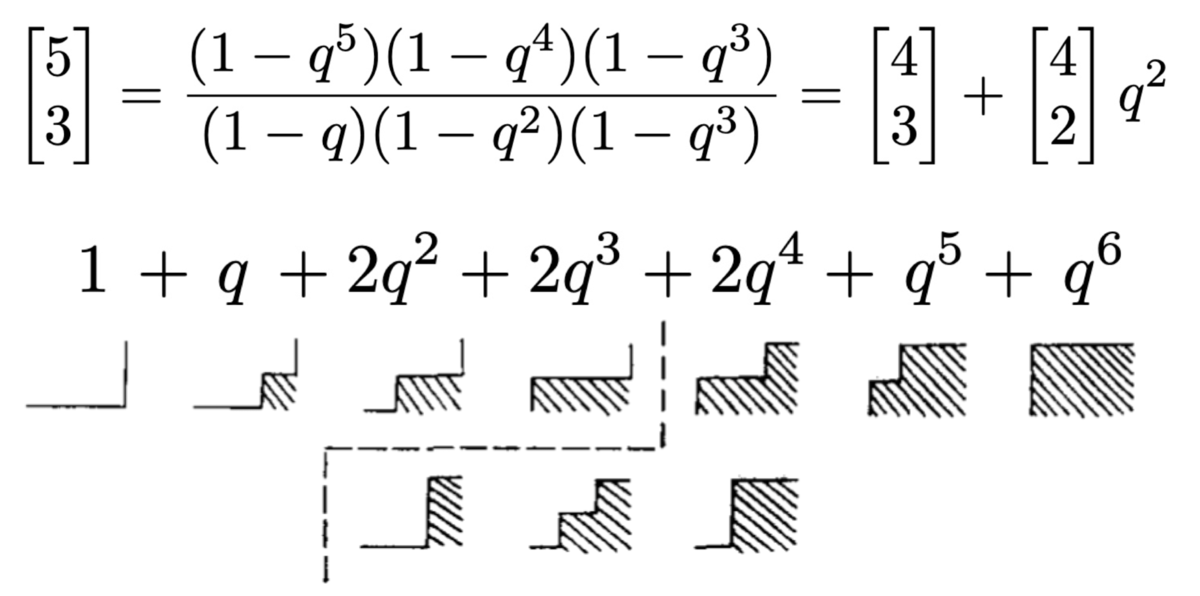訳者序
私がまだ高校一年生だったとき, 当時は中学生を担当していた私の恩師が, 道の数え上げに $q$ 二項係数が現れることを解説する課外授業を行うという告知を掲示板に貼っていたのを最近ふと思い出した. 老獪になった頭で久しぶりに色々考えて調べてみると, Pólya, G. (1969). On the number of certain lattice polygons. Journal of Combinatorial Theory, 6(1), 102-105. https://doi.org/10.1016/S0021-9800(69)80113-4. が初出だと判明した. 日本語で書かれた情報源にはほとんど記載が見受けられなかったので, 例のごとく 10 年留保を用いて翻訳することで紹介することにした. 過去の自分に対する数年越しの勝利というわけである. また, 10 年留保が適用できないので詳しくは紹介しないが, Pólya, G. & Alexanderson, G. L. (1971). Gaussian binomial coefficients. Elemente der Mathematik, 26(1971), 102-109. http://eudml.org/doc/141022. も参考になるだろう.
本文
F. Harary により伝達
二次元格子におけるさまざまな種類の経路数の明示的な表現を与える.
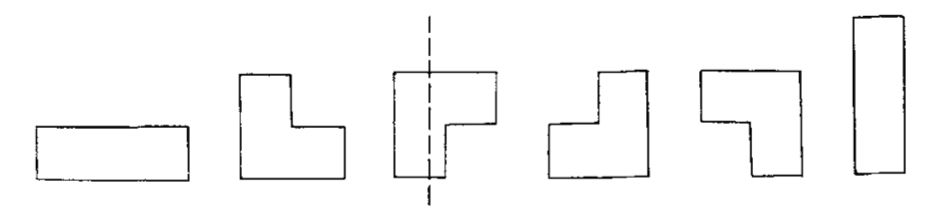
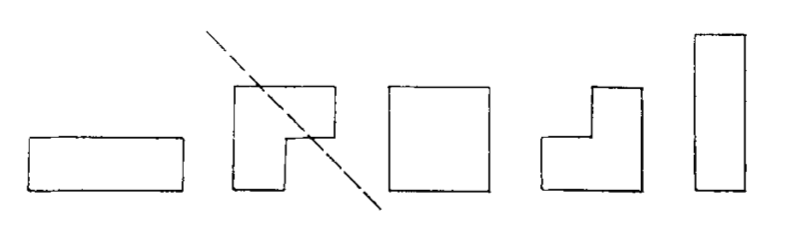
ある平面とそれに結び付けられた直交座標系を考える. どちらの座標も整数である点は格子点と呼ばれる. 重なる点のない閉多角形であって, 隣接する格子点を結ぶ長さ $1$ の線分からなるものは格子多角形 と呼ばれる (図 1 と図 2 を見よ). 二つの格子多角形が異なるものではないとみなされるのは, 一方を他方に重ね合わせるような平行移動が存在するときであり, かつそのときに限られる. ここで少しの間, 「異なる格子多角形 (different lattice polygon)」を dlp と略すことにし, $A_m$ を面積 $m$ の dlp の個数, $B_n$ を周長 $2n$ の dlp の個数, そして $C_{mn}$ を面積 $m$ で周長 $2n$ の dlp の個数としよう.
明らかに $$\sum _ {n}C _ {mn}=A _ {m},\quad\sum _ {m}C _ {mn}=B _ {n}$$ であり, $$C _ {mn}>0\text{ ならば }n-1\leqslant m\leqslant n ^ 2/4$$ であることが容易にわかる.
筆者の知る限り, $A_m$ も $B_n$ もまだ「明示的に」計算されたことはない. ここでは格子多角形のある種の部分集合に対する類似の量を計算しよう. 結論を簡潔に述べるためには定義が必要である.
重なる点をもたない閉平面曲線が方向 $d$ に関して凸であると呼ばれるのは, 曲線で囲まれた閉領域と方向 $d$ の任意の直線の交わりについて次の三つの場合だけが可能なときである: 交わりは空集合であるか, 一点のみからなるか, 一線分のみからなるかのいずれかである.
曲線が通常の意味で凸であることは, それがすべての方向に関して凸であることと同値である.
ここで二つの方向だけを考える: $90\degree$ つまり垂直方向と $-45\degree$ 方向である. 上で紹介した略語を用いて, $a_m$ を面積 $m$ の垂直方向に関して凸な dlp (図 1 参照) の個数とし,
$b_n$ を周長 $2n$ の $-45\degree$ 方向に関して凸な dlp (図 2 参照) の個数とし, $c_n$ を面積 $m$ で周長 $2n$ の $-45\degree$ 方向に関して凸な dlp (図 2 参照) の個数とする. 明らかに, $$\sum _ {m}c _ {mn}=b _ n$$ である.
筆者が得た結論は次の通りである:
$$\begin{align*} \sum _ {m=1} ^ {\infty} a _ m x ^ m &= x+2x ^ 2+6x ^ 3+19x ^ 4+61x ^ 5+\cdots\\ &=\frac{x(1-x) ^ 3}{1-5x+7x ^ 2-4x ^ 3}\tag{1}\\ b _ n &=\frac{1}{4n-2}\binom{2n}{n}\tag{2}\\ \sum _ {n=1} ^ {\infty}\sum _ {m}c _ {mn}q ^ {m}x ^ {n} &= \cdots+q ^ {-1}x ^ 2+2x+qx ^ 2+2q ^ 2x ^ 3+(q ^ 4+4q ^ 3)x ^ 4+\cdots\\ &=1-\frac{1}{1+P _ 1(q)x+P _ 2(q)x ^ 2+P _ 3(q)x ^ 3+\cdots}\quad\text{(3)} \end{align*}$$
ここで, 定義より $$c _ {01}=2,\quad c _ {-mn}=c _ {mn},\newline P _ n(q)=\sum _ {r=0} ^ {n}\begin{bmatrix}n\\r\end{bmatrix} ^ 2q ^ {-r(n-r)}$$ であり, $$\begin{bmatrix}n\\r\end{bmatrix}=\frac{(1-q ^ n)(1-q ^ {n-1})\cdots(1-q ^ {n-r+1})}{(1-q)(1-q ^ 2)\cdots(1-q ^ r)}$$ であり, これは Gauss 二項係数*1 [訳注: 現代的には $q$ 二項係数と呼ばれる] の標準的な記法である. (3) で述べられた式は純粋に形式的に理解することができる. 実際, この級数は $$|q|=1,\quad|x|<1/4$$ という条件を充たすすべての複素数値 $q$ と $x$ について収束する. 考えている三つの式はすべて $q$ と $q ^ {-1}$ を入れ替えても変化しない.
ここで「$a _ n$ という数は再帰的に計算できたり三次方程式の三つの根を用いて表せたりする」という (1) の自明な帰結について立ち入る必要はないだろう.
上述の結果の証明は, 本論文の続きで行われる予定である*2.
今は一つだけ注意を付け加えるに留めたい. 通常の二項係数 $\binom{n}{r}$ が格子において持つ意味合いは広く知られている*3. それは格子 (「道路網」) の原点 $(0,0)$ から点 $(r,n-r)$ までを結ぶ最短ジグザグ経路の数である. Gauss 二項係数を考えることで, この改良版を得ることができる. 上で定義したように, ${n\brack r}$ は変数 $q$ の有理関数のように見えるが, しかしながら実は $q$ の正整数係数多項式なのである: $$\begin{bmatrix}n\\r\end{bmatrix}=\sum _ {\alpha=0} ^ {r(n-r)} N _ {nr\alpha}q ^ {\alpha}.\tag{4}$$
$q=1$ では Gauss 二項係数は通常の二項係数に移行する: $$\binom{n}{r}=\sum _ {\alpha=0} ^ {r(n-r)} N _ {nr\alpha}.$$
本論文の続きにおいて筆者は, それ自体が興味を持つに値するかもしれない次の事実を用いるだろう:
補題. $\binom{n}{r}$ により数え上げられる格子内のジグザグ経路であってその下の面積が $\alpha$ になるものの個数は $N _ {nr\alpha}$ に等しい.
「経路の下の」面積 $\alpha$ は, 経路と, 水平な座標軸 $y=0$ と, 直線 $x=r$ に囲まれている. 図 3 は $n=5$, $r=3$ の場合を図示している. 図 3 の破線は特定の $\binom{4}{3}$ 経路とそれ以外の $\binom{4}{2}$ 経路を分けており, これはこの補題を示すための手がかりを極めて明確に与えている: 証明は$$\begin{bmatrix}n+1\\r\end{bmatrix}=\begin{bmatrix}n\\r\end{bmatrix}+\begin{bmatrix}n\\r-1\end{bmatrix}q ^ {n+1-r}$$ という漸化式 [訳注: Pascal の三角形の $q$ 類似] に基づいて数学的帰納法を用いるのである.