はじめに
この記事では Evan Chen 氏による Some Notes on Constructing Diagrams の §6 Computer-Generated Figures にある内容を、いくつかの補足を加えつつ日本語圏の中高生を想定読者として紹介します。
なお、TikZ を用いた作図も可能であり、たとえば CTAN: Package tkz-euclide が強力なパッケージとして存在していますが、少なくもアメリカの数オリ界隈では Asymptote の方が有力なように見えます(たとえば AoPS では Asymptote で図を記述することが可能です)。
GeoGebra
まずはここで GeoGebra Classic 5 を手に入れましょう。自由に使えばいいわけですが、せっかくなので「ある点 $A$ から直線 $BC$ におろした垂線の足」を定義してみましょう。
ここから Input に D = Intersect[Line[B, C], PerpendicularLine[A, Line[B, C]]] と打ち込みます。
メニューバーから Tools > Create New Tools ... と開きます。
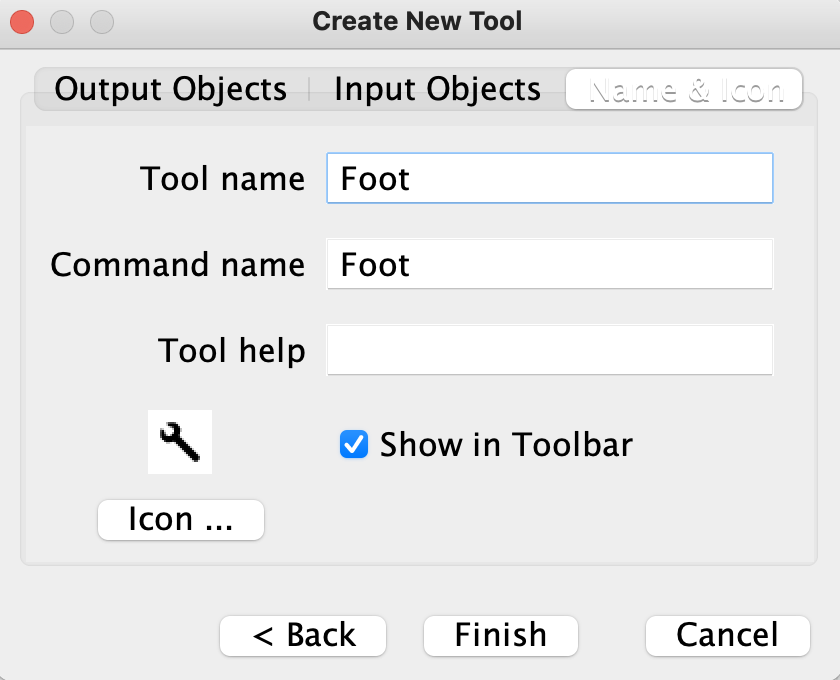
あとは Finish を押して完成です。
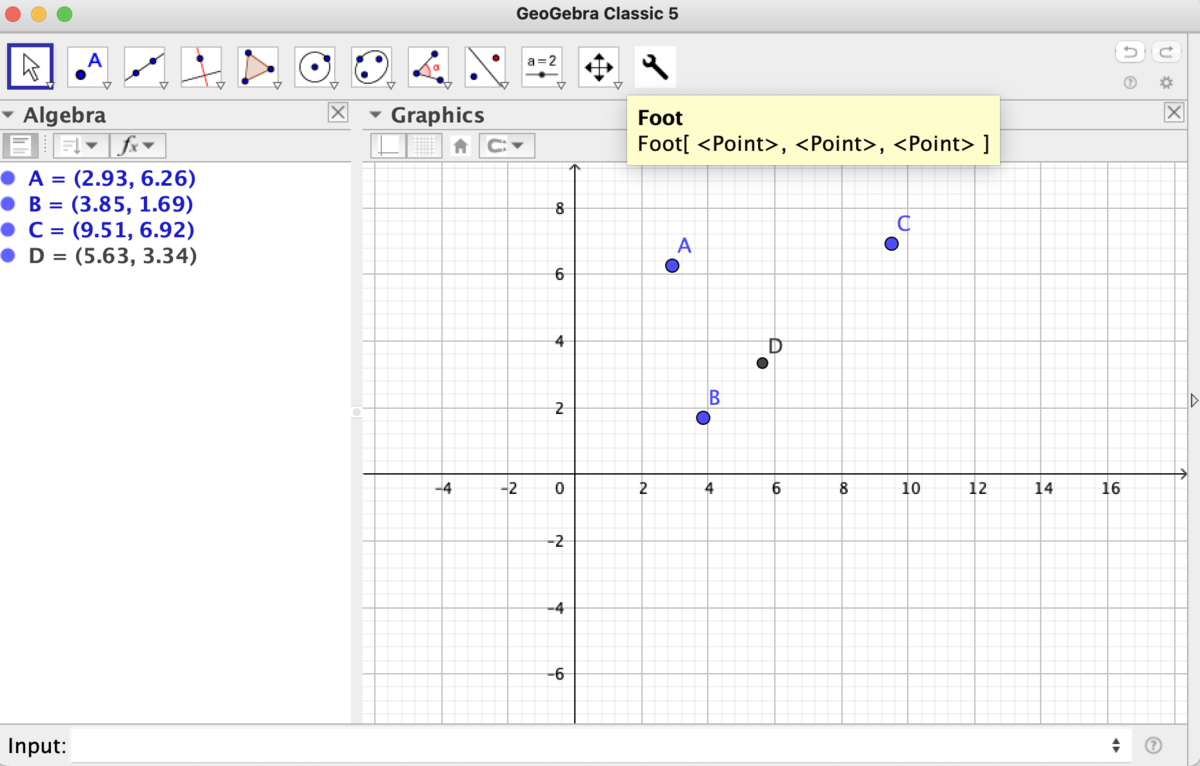
垂線の足が定義できたので、円と交わる直線の二交点の一方を他方から計算することを考えてみましょう。実は、GeoGebra はそのまま点を打ち込めばそれがベクトルと解釈されるので、次のような図では D = -C + 2Foot[B, A, C] と打ち込めばよいことになります(理由は図とにらめっこすれば明らかです)。
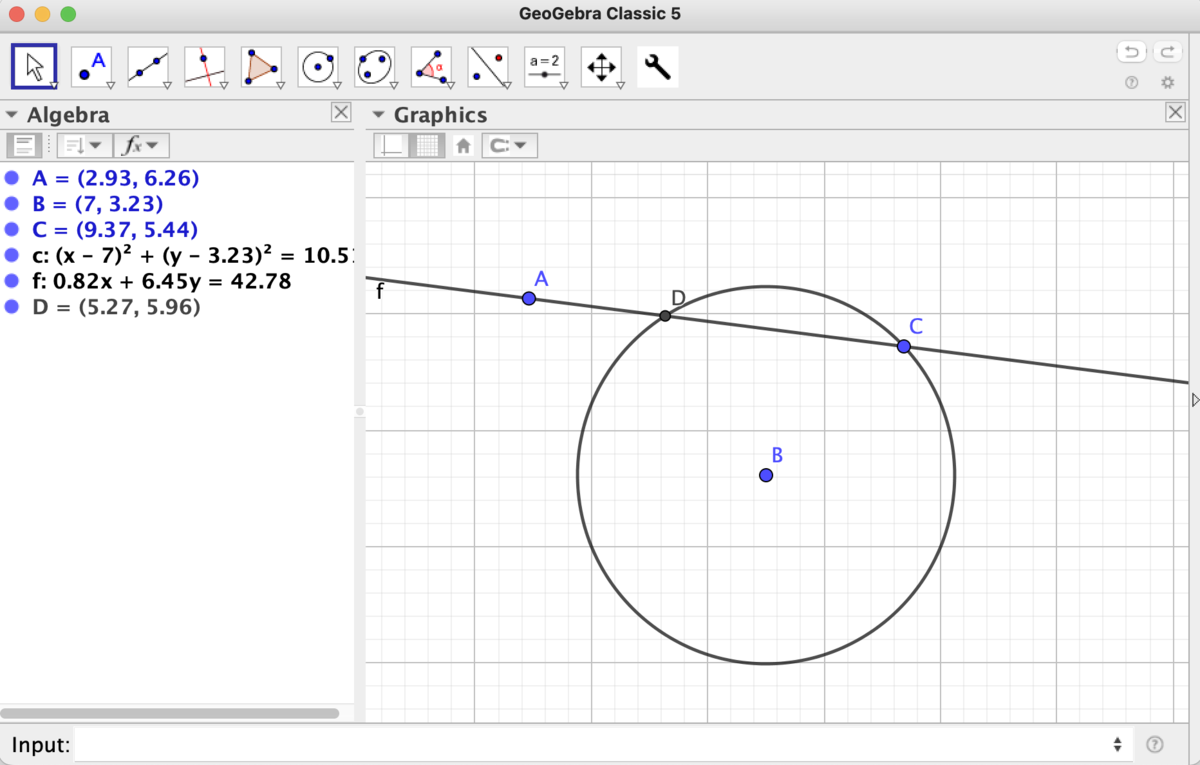
この技術を使えば基本的にどんな初等幾何の主張の真偽も確認できますが、その際に重要となるテクニックとして「初期条件の点や直線を自由に動かして様々な位置関係で実験すべき」だということが挙げられます。
Asymptote
何はともあれ、最初は TeX Wiki を参照しておきましょう。自分は brew install asymptote でインストールしました。
無事インストールできたら、olympiad.asy と cse5.sty を Evan Chen 氏のリポジトリから入手して asymptote > 2.81 > share > asymptote の中に入れましょう。
GeoGebra で作った図から File > Export > Graphics View as Asymptote ... でコードが生成できますが、その場合は細かすぎる小数点以下の値を削ぎ落とす作業を行った方がよいです。
具体例として Evan Chen 氏の例を引用してみましょう。
import olympiad;
import cse5;
defaultpen(fontsize(10pt));
usepackage("amsmath");
usepackage("amssymb");
settings.tex="latex";
settings.outformat="pdf";
size(12cm);
pair A = dir(120);
pair B = dir(210);
pair C = dir(330);
draw(A--B--C--cycle, red+1.3);
pair I = incenter(A, B, C);
pair D = foot(I, B, C);
pair E = foot(I, C, A);
pair F = foot(I, A, B);
pair P = foot(D, E, F);
pair Y = extension(B, P, A, C);
pair Z = extension(C, P, A, B);
draw(incircle(A, B, C), dashed+red);
filldraw(circumcircle(A, B, C), opacity(0.2)+lightcyan, blue);
filldraw(circumcircle(A, E, F), opacity(0.2)+paleblue, blue);
filldraw(circumcircle(A, Y, Z), opacity(0.2)+lightgreen, blue);
draw(B--Y, brown);
draw(C--Z, brown);
draw(D--E--F--cycle , red);
draw(D--P, red);
pair X = foot(A, P, I);
draw(I--X, orange);
pair K = foot(A, B, C);
draw(A--K, red);
pair Q = extension(P, I, A, K);
dot("$A$", A, dir(A));
dot("$B$", B, dir(B));
dot("$C$", C, dir(C));
dot("$I$", I, dir(-90));
dot("$D$", D, dir(D));
dot("$E$", E, dir(10));
dot("$F$", F, dir(190));
dot("$P$", P, dir(-90));
dot("$Y$", Y, dir(50));
dot("$Z$", Z, dir(200));
dot("$X$", X, dir(X));
dot("$Q$", Q, dir(45));
まずは最も原始的なやり方で行きましょう。上述のコードを test.asy というファイル名で保存したとします。次に test.asy のあるディレクトリまで移動してから asy -f pdf -V test と打ちましょう。
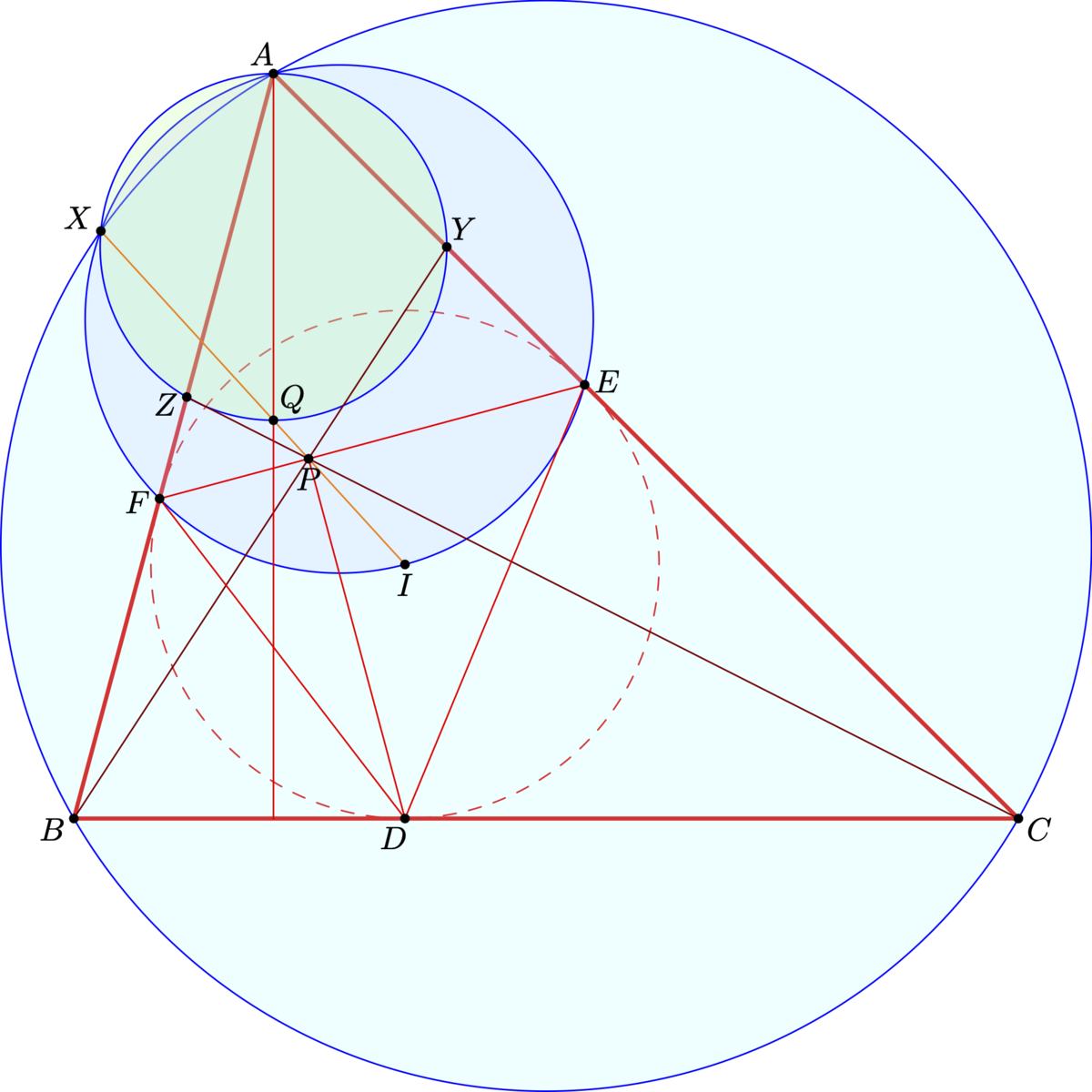
なかなか凄いですね。
他にも色々と便利な活用法があるのですが、環境依存になりやすいようなので TeX Wiki を参照してみてください。また、Evan Chen 氏のハンドアウトを漁れば多くの実装例が眺められますし、数オリでは Asymptote のソースコードの蓄積はかなり多いようです。